反射模型

在渲染方程中提到过一个非常重要的概念，双向反射分布函数BRDF，它描述了一个物体在点p处将${\omega }_i$方向的入射光反射到${\omega }_o$方向的能力。BRDF是一个简化的模型，只考虑了光的反射，现实中的光照更加复杂，除了反射还有折射、透射等，尽管在程序中没有办法完全模拟出现实世界的光照效果，我们还是希望有一个模型可以尽可能地逼近现实。反射模型（Reflection Models）就是用来完成这个工作的（尽管它还是叫做反射模型），它描述了光照与物体交互的效果，是渲染中不可缺少的一部分。

基本理念

通常来说，反射包括以下四种类型：

• 漫反射：物体将入射光线均匀地反射到四周。
• 光泽反射：物体将入射光线向特定的方向散射，从散射方向观察物体可以看到明显的“高光”。
• 全反射（完美反射）：像镜面一样，将入射光线全部反射至反射方向。
• 逆射：将入射光线沿着入射反向散射射回去，比如天鹅绒材质，会在物体表面形成一层“光泽”。
  物体并不是只进行一种类型的反射，通常是多种反射的混合，但是根据能量守恒定理，反射出的所有光线能量不会大于入射的光线能量。
  光线反射还有一种概念是各向同性和各向异性，对于各向同性的反射，沿着反射点的法线旋转，从不同角度观察到的反射效果是一样的，而对于各向异性的反射，反射的效果会不同。最常见的包含这种反射的物体就是磨砂金属。

反射模型的描述

通常使用BxDF函数来描述反射模型，字母x并没有特殊的含义，是因为几种函数的名称只有第二个字母不一样，BxDF可以分为以下几类：

• BRDF（双向反射分布函数，Bidirectional Reflectance Distribution Function）：用于非透明材质的光照计算。
• BTDF（双向透射分布函数，Bidirectional Transmission Distribution Function）：用于透明材质的光照计算。折射光穿透介质进入另外一种介质时的光照计算模型，只对有透明度的介质适用。
• BSDF（双向散射分布函数，Bidirectional Scattering Distribution Function）：实际上是BRDF和BTDF的综合体。
• BSSRDF（双向表面散射分布函数，Bidirectional Surface Scattering Reflectance Distribution Function）：它常用于模拟透明材质，目前是主流技术。它和BRDF的不同之处在于，BSSRDF可以再现光线透射材质的效果，还可以指定不同的光线入射位置和出射位置。
  各种BxDF函数都是以下形式：

$$f({\omega }_i,{\omega }_o,p)=...$$

BxDF接口设计

渲染系统中BxDF的接口描述了BxDF的通用函数，具体的设计如下：

class BxDF
    : 
{
  public:
       BxDFFlags Flags() const;
       using TaggedPointer::TaggedPointer;
       
       std::string ToString() const;
       SampledSpectrum f(Vector3f wo, Vector3f wi, TransportMode mode) const;
       pstd::optional<BSDFSample>
       Sample_f(Vector3f wo, Float uc, Point2f u,
                TransportMode mode = TransportMode::Radiance,
                BxDFReflTransFlags sampleFlags = BxDFReflTransFlags::All) const;
       Float PDF(Vector3f wo, Vector3f wi, TransportMode mode,
                 BxDFReflTransFlags sampleFlags = BxDFReflTransFlags::All) const;
       SampledSpectrum rho(Vector3f wo, pstd::span<const Float> uc,
                           pstd::span<const Point2f> u2) const;
       SampledSpectrum rho(pstd::span<const Point2f> u1,
                                  pstd::span<const Float> uc2,
                                       pstd::span<const Point2f> u2) const;
       void Regularize();
};

下面是每个函数的含义。

BxDFFlags Flags()

返回此物体BxDF标志，它由物体的材质决定，BxDFFlags的定义为：

enum BxDFFlags {
    Unset = 0,
    Reflection = 1 << 0,
    Transmission = 1 << 1,
    Diffuse = 1 << 2,
    Glossy = 1 << 3,
    Specular = 1 << 4,
       DiffuseReflection = Diffuse | Reflection,
       DiffuseTransmission = Diffuse | Transmission,
       GlossyReflection = Glossy | Reflection,
       GlossyTransmission = Glossy | Transmission,
       SpecularReflection = Specular | Reflection,
       SpecularTransmission = Specular | Transmission,
       All = Diffuse | Glossy | Specular | Reflection | Transmission
};

Reflection和Transmission决定了光线是进行反射还是透射，下面的Diffuse，Glossy和Specular决定了反射（透射）的类型，这里将逆射并入了Glossy类型。

f函数

这是BxDF的核心函数，它接受出射光线方向wo，入射光线方向wi以及光线传输模式mode，返回BxDF函数的值。
按照BxDF函数的定义，f函数应该还需要反射发生的具体的位置点p，但是在程序设计中，必然是先找到了光线与物体的点才能找到该点的材质，进而找到使用BxDF，所以这里就不需要点p作为入参。
它的返回值SampledSpectrum部分定义如下：

static constexpr int NSpectrumSamples = 4;
 
class SampledSpectrum {
  public:
    ... 
  private:
    pstd::array<Float, NSpectrumSamples> values;
};

它是一个数组，每个元素包含了4个float值，数组长度代表了采样光谱的数量，后续可以用它们对光谱进行采样，其中每一个元素可以看作一个颜色。
mode参数用来指示出射方向是朝向相机还是朝向光源，或者是入射方向的相反方向，后续可以用来处理不对称的散射，它的定义如下：

enum class TransportMode { Radiance, Importance };

Sample_f函数

Sample_f函数用来提供在已知光线出射方向时的入射方向及其pdf，这个说法看上去有点奇怪，其实在光线追踪算法中，我们是按照光线传输的逆方向发射光线的，光线在人眼（相机）处产生，根据光路的可逆性，最终计算的结果与正常的光照相同。这样做产生一个后果，我们是先知道了出射方向的光线（它是相机发射光线的反方向），然后再去求入射光线的方向。
Sample_f函数的作用很明显，BxDF的函数值是在渲染方程积分项之中的，对它的入射光线方向采样必然要使用到函数分布的pdf。在现实中这种方式也是非常合理的，当物体进行全反射时（比如镜面），除了出射方向的反射方向，其他方向的入射光线是不提供任何贡献的，它们的pdf应该等于0。
Sample_f函数定义如下：

pstd::optional<BSDFSample>
Sample_f(Vector3f wo, Float uc, Point2f u,
         TransportMode mode = TransportMode::Radiance,
         BxDFReflTransFlags sampleFlags = BxDFReflTransFlags::All) const;

wo为出射方向，uc和u是随机值，比如可以使用uc来决定进行透射还是反射，使用u来选定入射方向（极坐标系）,mode上面已经介绍过，sampleFlags强制指定进行透射还是进行反射，或者二者都有。

enum class BxDFReflTransFlags {
    Unset = 0,
    Reflection = 1 << 0,
    Transmission = 1 << 1,
    All = Reflection | Transmission
};

函数的返回值为pstd::optional<BSDFSample>，这表示采样是有可能失败的，比如在不透明的物体上进行透射。
BSDFSample包含了此次采样的结果，它的定义如下，

struct BSDFSample {
    // 构造函数省略
    SampledSpectrum f;    // 此次采样的结果，BxDF的函数值
    Vector3f wi;          // 入射方向
    Float pdf = 0;        // 此次采样立体角的pdf值
    BxDFFlags flags;      // 样本特征，上面有介绍相关定义
    Float eta = 1;        // IOR(折射率)
    bool pdfIsProportional = false;  // 某些随机光路的BxDF会使用到，大多数情况下为false
};

同样，有一些工具函数来快速判断采样的样本特征，

bool IsReflection() const { return pbrt::IsReflective(flags); }
bool IsTransmission() const { return pbrt::IsTransmissive(flags); }
...

PDF函数

PDF函数返回BxDF指定出射和入射方向的pdf值，

Float PDF(Vector3f wo, Vector3f wi, TransportMode mode,
          BxDFReflTransFlags sampleFlags = BxDFReflTransFlags::All) const;

mode参数和sampleFlags参数的含义与Sample_f相同。

rho

这个函数是半球面反射的相关函数，使用蒙特卡洛积分计算物体表面的某个点的辐射率，它有两种类型的重载。
第一种函数提供出射方向wo和采样点数对应的样本，计算spectrum，

SampledSpectrum BxDF::rho(Vector3f wo, pstd::span<const Float> uc,
                          pstd::span<const Point2f> u2) const {
    SampledSpectrum r(0.);
    for (size_t i = 0; i < uc.size(); ++i) {
           pstd::optional<BSDFSample> bs = Sample_f(wo, uc[i], u2[i]);
           if (bs)
               r += bs->f * AbsCosTheta(bs->wi) / bs->pdf;
 
    }
    return r / uc.size();
}

uc和u2是样本值，uc是一维的样本，u2是二维的样本。
其中使用的函数AbsCosTheta：

Float AbsCosTheta(Vector3f w) { return std::abs(w.z); }

因为向量是定义在局部空间中的，该点的法线作为坐标系的z轴，而$cos\theta$是计算该向量与法线的夹角，所以向量z坐标乘以向量长度即为$cos\theta$，由于wi是归一化的单位向量，所以直接取z坐标的值即可。这里取得是z坐标的绝对值，说明向量位于法线负半球时，与正半球得到的结果相同。
使用公式来表示：

$${\rho }_{hd}({\omega }_o)={\int }_{H^2(n)}f(p,{\omega }_o,{\omega }_i)|cos{\theta }_i|d{\omega }_i$$

第二种函数并不直接提供wo，而是随机在法线的半球面选择一个wo方向，用于计算所有方向的入射光都相同时半球面的反射率，

SampledSpectrum BxDF::rho(pstd::span<const Point2f> u1,
        pstd::span<const Float> uc, pstd::span<const Point2f> u2) const {
    SampledSpectrum r(0.f);
    for (size_t i = 0; i < uc.size(); ++i) {
           Vector3f wo = SampleUniformHemisphere(u1[i]);
           if (wo.z == 0)
               continue;
           Float pdfo = UniformHemispherePDF();
           pstd::optional<BSDFSample> bs = Sample_f(wo, uc[i], u2[i]);
           if (bs)
               r += bs->f * AbsCosTheta(bs->wi) * AbsCosTheta(wo) / (pdfo * bs->pdf);
 
    }
    return r / (Pi * uc.size());
}

可以看到wo是从SampleUniformHemisphere函数采样获得的。SampleUniformHemisphere用于在半球面上均匀采样，它的实现为：

Vector3f SampleUniformHemisphere(Point2f u) {
    Float z = u[0];
    Float r = SafeSqrt(1 - Sqr(z));
    Float phi = 2 * Pi * u[1];
    return {r * std::cos(phi), r * std::sin(phi), z};
}

这里传入一个二维随机数u，生成半球面上的三维向量(x, y, z)，具体的实现原理先忽略，就是根据蒙特卡洛积分和采样中的重要性采样方法推导出来的。
UniformHemispherePDF是半球面上均匀采样的PDF，它是一个常数$1/2\pi$，

Float UniformHemispherePDF() { return Inv2Pi; }

这个函数使用公式来表示：

$${\rho }_{hh}=\frac{1}{\pi }{\int }_{H^2(n)}{\int }_{H^2(n)}f(p,{\omega }_o,{\omega }_i)|cos{\theta }_{o}cos{\theta }_i|d{\omega }_{o}d{\omega }_i$$

表示BxDF在入射光在所有方向都相同时，整个半球表面的反射率。

BSDF接口设计

BSDF接口是BxDF接口的简单封装，包含了从渲染空间（可能是世界空间也可能是相机空间）转换的局部空间的变换方法，因为通常BSDF的计算在局部空间完成。

class BSDF {
  public:
       ...
  private:
       BxDF bxdf;
       Frame shadingFrame;
 
};

BSDF并不继承BxDF接口，而是包含一个BxDF成员变量，shadingFrame保存当前渲染帧的信息。
下面是BSDF接口中包含几个重要的方法。

构造函数

BSDF() = default;
BSDF(Normal3f ns, Vector3f dpdus, BxDF bxdf)
    : bxdf(bxdf),
      shadingFrame(Frame::FromXZ(Normalize(dpdus), Vector3f(ns))) {}

接受着色点的法线和bxdf变量，以及dpdu（目前只关心法线即可）。

坐标转换

Vector3f RenderToLocal(Vector3f v) const { return shadingFrame.ToLocal(v); }
Vector3f LocalToRender(Vector3f v) const {
    return shadingFrame.FromLocal(v);
}

用来进行渲染空间与局部空间的相互转换。

f函数

SampledSpectrum f(Vector3f woRender, Vector3f wiRender,
                  TransportMode mode = TransportMode::Radiance) const {
    Vector3f wi = RenderToLocal(wiRender), wo = RenderToLocal(woRender);
    if (wo.z == 0) return {};
    return bxdf.f(wo, wi, mode);
}

计算指定出射和入射方向的BSDF函数值，将向量变换到局部空间后，调用bxdf的接口进行计算。
它还要另一种模版形式，在指定了具体的bxdf类型后直接调用该类型的f函数，

template <typename BxDF>
SampledSpectrum f(Vector3f woRender, Vector3f wiRender,
                  TransportMode mode = TransportMode::Radiance) const {
    Vector3f wi = RenderToLocal(wiRender), wo = RenderToLocal(woRender);
    if (wo.z == 0) return {};
    const BxDF *specificBxDF = bxdf.CastOrNullptr<BxDF>();
    return specificBxDF->f(wo, wi, mode);
}

Sample_f函数

pstd::optional<BSDFSample> Sample_f(
        Vector3f woRender, Float u, Point2f u2,
        TransportMode mode = TransportMode::Radiance,
        BxDFReflTransFlags sampleFlags = BxDFReflTransFlags::All) const {
    Vector3f wo = RenderToLocal(woRender);
    if (wo.z == 0 ||!(bxdf.Flags() & sampleFlags)) return {};
       pstd::optional<BSDFSample> bs = bxdf.Sample_f(wo, u, u2, mode, sampleFlags);
       if (!bs || !bs->f || bs->pdf == 0 || bs->wi.z == 0)
           return {};
       bs->wi = LocalToRender(bs->wi);
       return bs;
}

同样也是调用bxdf的Sample_f函数，这里增加了坐标系的转换，以及对采样结果的检查，如果采样失败或者pdf为0，亦或是采样的wi与法线垂直(bs→wi.z == 0)，那么不会返回采样结果。

PDF函数

Float PDF(Vector3f woRender, Vector3f wiRender,
          TransportMode mode = TransportMode::Radiance,
          BxDFReflTransFlags sampleFlags = BxDFReflTransFlags::All) const {
    Vector3f wo = RenderToLocal(woRender), wi = RenderToLocal(wiRender);
    if (wo.z == 0) return 0;
    return bxdf.PDF(wo, wi, mode, sampleFlags);
}

检测wo方向后调用bxdf的PDF函数。

漫反射（Diffuse Reflection）

漫反射是最简单的一种反射模型，它假设物体表面接受到光照后，会向四面八方均匀地反射。通常这种模型被称为Lambertian反射模型，它的BSDF函数是一个常数。即

$$f_{lambertian}=C$$

假设物体的反射率为R（通常这个反射率就是物体的基础颜色），根据能量守恒定理：

$${\int }_{H^2(n)}Ccos\theta d\omega ={\int }_0^{2\pi }{\int }_0^{\frac{\pi }{2}}Ccos\theta sin\theta d\theta d\varphi =R$$

可以解得

$$C=\frac{R}{\pi }$$

所以

$$f_{lambertian}=\frac{R}{\pi }$$

DiffuseBxDF的具体设计：

class DiffuseBxDF {
  public:
    ...
  private:
    SampledSpectrum R;
};

R为物体的反射率（反照率），通常是物体的基础颜色。

f函数

SampledSpectrum f(Vector3f wo, Vector3f wi, TransportMode mode) const {
    if (!SameHemisphere(wo, wi))
        return SampledSpectrum(0.f);
    return R * InvPi;
}

如果wo和wi在同一半球，则返回$R/\pi$，否则返回0。

bool SameHemisphere(Vector3f w, Vector3f wp) {
    return w.z * wp.z > 0;
}

Sample_f函数

pstd::optional<BSDFSample> Sample_f(
        Vector3f wo, Float uc, Point2f u, TransportMode mode,
        BxDFReflTransFlags sampleFlags = BxDFReflTransFlags::All) const {
    if (!(sampleFlags & BxDFReflTransFlags::Reflection))
        return {};
    Vector3f wi = SampleCosineHemisphere(u);
    // 保证wo和wi在同一半球
    if (wo.z < 0) 
       wi.z *= -1;
    Float pdf = CosineHemispherePDF(AbsCosTheta(wi));
    return BSDFSample(R * InvPi, wi, pdf, BxDFFlags::DiffuseReflection);
}

通过SampleCosineHemisphere函数采样出方向wi，这里的SampleCosineHemisphere函数是对半球上的$cos\theta$项进行采样，采样算法与上面的SampleUniformHemisphere相同，同样是重要性采样方法。然后使用CosineHemispherePDF计算$f=cos\theta$在半球面上的pdf。
按理来说，根据渲染方程中的描述，这里的采样只涉及到BxDF项，$cos\theta$项是不需要考虑的，但是实践证明，将$cos\theta$项加入BxDF项一起考虑会得到更佳的渲染效果，从上面$f_{lambertian}$的推导也可以看出来，$cos\theta$已经被考虑到了BxDF函数中，所以这里采样时，不是因为BRDF是常数就进行常数的采样，而是针对$\cos \theta$进行采样。后面的各类BSDF和BRDF模型也会遵循此原则。
SampleCosineHemisphere和CosineHemispherePDF实现如下：

Vector3f SampleCosineHemisphere(Point2f u) {
    Point2f d = SampleUniformDiskConcentric(u);
    Float z = SafeSqrt(1 - Sqr(d.x) - Sqr(d.y));
    return Vector3f(d.x, d.y, z);
}
 
Float CosineHemispherePDF(Float cosTheta) {
    return cosTheta * InvPi;
}

关于$cos\theta$在半球面采样的pdf计算，根据重要性采样（Importance Sampling）中介绍的方法可以计算出$pdf=\frac{\cos \theta }{\pi }$。

PDF函数

Float PDF(Vector3f wo, Vector3f wi, TransportMode mode,
          BxDFReflTransFlags sampleFlags = BxDFReflTransFlags::All) const {
    if (!(sampleFlags & BxDFReflTransFlags::Reflection) ||
        !SameHemisphere(wo, wi))
        return 0;
    return CosineHemispherePDF(AbsCosTheta(wi));
}

根据上面的原则，这里也是返回CosineHemispherePDF(AbsCosTheta(wi))。

镜面反射和透射的原理

IOR

IOR（Index of Refraction）意味折射率，它反应了光线进入物体时，光速的衰减情况，比如一个材质的IOR为2，那就说明光线进入这个材质后，传播速度会变为光速的一半。通常情况下材质的IOR在1.0到2.5之间。
IOR通常使用$\eta$来表示。
下面是一些常见介质的IOR。

介质	Index of refraction（$\eta$）
真空	1.0
冰	1.31
水(20摄氏度)	1.333
玻璃	1.5-1.6
钻石	2.42

镜面反射定律

假设入射光的角度为(${\theta }_i$,${\varphi }_i$)，当它发生镜面反射时，其反射方向为入射方向绕法线旋转180度，使用公式来表示：

$${\theta }_r={\theta }_i{\varphi }_r={\varphi }_i+\pi$$

如果使用立体角$\omega$来表示，反射方程推导过程如下。
假设入射方向为$\omega$，反射方向与入射方向、法线必然位于同一平面，在这个平面上，将$\omega$分解：

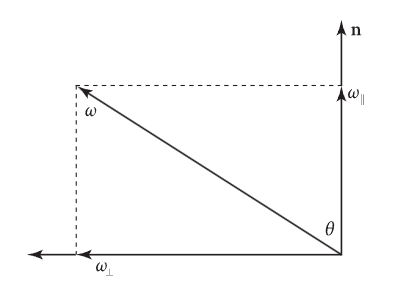
则有：

$$\begin{array}{rl}& \\ {\omega }_{||}& =n\cdot cos\theta =(n\cdot \omega )n\\ {\omega }_{\perp }& =\omega -{\omega }_{||}=w-(n\cdot \omega )n\end{array}$$

根据镜面反射定律，有

$$\begin{array}{rl}& \\ {\omega }_{r||}& ={\omega }_{||}=(n\cdot \omega )n\\ {\omega }_{r\perp }& =-{\omega }_{\perp }=(n\cdot \omega )n-\omega \end{array}$$

最终反射方向

$$\begin{array}{rl}& \\ {\omega }_r& ={\omega }_{r||}+{\omega }_{r\perp }\\ & =(n\cdot \omega )n-\omega +(n\cdot \omega )n\\ & =2(n\cdot \omega )n-\omega \end{array}$$

使用代码实现：

Vector3f Reflect(Vector3f wo, Vector3f n) {
    return -wo + 2 * Dot(wo, n) * n;
}

折射定律

当入射光以角度为(${\theta }_i$,${\varphi }_i$)照射物体并发生折射时，折射光线方向与两边介质的IOR相关，具体为

$${\eta }_{i}sin{\theta }_i={\eta }_{t}sin{\theta }_t{\varphi }_t={\varphi }_i+\pi$$

这就是折射定律。
为了方便，通常使用相对折射率来表示折射定律，相对折射率定义为

$$\eta =\frac{{\eta }_t}{{\eta }_i}$$

因此有

$$sin{\theta }_i=\eta sin{\theta }_t$$

在多数情况下，光线追踪算法的光线是从真空射入物体的，所以${\eta }_i=1$，此时$\eta ={\eta }_t$，计算更加方便。
同样，如果使用立体角来表示，如下图

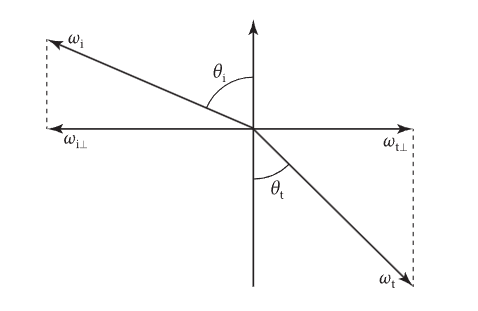
则有

$$\begin{array}{rl}& \\ {\omega }_{t||}& =-cos{\theta }_{t}n\\ {\omega }_{t\perp }& =-\frac{{\omega }_{i\perp }}{\eta }=\frac{-{\omega }_i+({\omega }_i\cdot n)n}{\eta }\end{array}$$

最终折射方向

$$\begin{array}{rl}& \\ {\omega }_t& ={\omega }_{t\perp }+{\omega }_{t||}\\ & =-\frac{{\omega }_i}{\eta }+[\frac{({\omega }_i\cdot n)}{\eta }-cos{\theta }_t]n\end{array}$$

代码实现：

bool Refract(Vector3f wi, Normal3f n, Float eta, Float *etap, Vector3f *wt) {
    Float cosTheta_i = Dot(n, wi);
    // cos theta小于0表示光线从物体向外发生折射
    if (cosTheta_i < 0) {
        eta = 1 / eta;
        cosTheta_i = -cosTheta_i;
        n = -n;
    }
 
    Float sin2Theta_i = std::max<Float>(0, 1 - Sqr(cosTheta_i));
    Float sin2Theta_t = sin2Theta_i / Sqr(eta);
    // sin2Theta_t >= 1表示发生全反射
    if (sin2Theta_t >= 1)
        return false;
 
    Float cosTheta_t = SafeSqrt(1 - sin2Theta_t);
 
    *wt = -wi / eta + (cosTheta_i / eta - cosTheta_t) * Vector3f(n);
    // 根据需要提供eta
    if (etap)
        *etap = eta;
 
    return true;
}

菲涅尔方程

上面的反射定律和折射定律描述了光线发生镜面反射和折射时出射光的方向，现在需要知道出射光的能量大小。
当光线照射到一个物体上时，通常会同时发生反射和折射，菲涅尔方程描述了光线的反射率，即光线有多少能量被反射。
菲涅尔方程与入射光和折射光的振幅有关，其中平行方向和垂直方向的计算方式也不相同。而振幅与光的折射率和入射角相关，具体的方程为：

$$\begin{array}{r}{r}_{||}=\frac{E_r^{||}}{E_i^{||}}=\frac{{\eta }_{t}cos{\theta }_i-{\eta }_{i}cos{\theta }_t}{{\eta }_{t}cos{\theta }_i+{\eta }_{i}cos{\theta }_t}\\ r_{\perp }=\frac{E_r^{\perp }}{E_i^{\perp }}=\frac{{\eta }_{i}cos{\theta }_i-{\eta }_{t}cos{\theta }_t}{{\eta }_{i}cos{\theta }_i+{\eta }_{t}cos{\theta }_t}\end{array}$$

按照之前的表示方式，令$\eta =\frac{{\eta }_t}{{\eta }_i}$。则上面的方程可以表示为：

$$\begin{array}{r}{r}_{||}=\frac{\eta cos{\theta }_i-cos{\theta }_t}{\eta cos{\theta }_i+cos{\theta }_t}\\ r_{\perp }=\frac{cos{\theta }_i-\eta cos{\theta }_t}{cos{\theta }_i+\eta cos{\theta }_t}\end{array}$$

最终的菲涅尔反射率由两个方向的振幅比值结合起来：

$$F_r=\frac{1}{2}(r_{||}^2+r_{\perp }^2)$$

这个比例就是光线发生反射时反射光线所占的能量比例。
代码实现：

Float FrDielectric(Float cosTheta_i, Float eta) {
    cosTheta_i = Clamp(cosTheta_i, -1, 1);
    // cosTheta_i 小于0时反转朝向
    if (cosTheta_i < 0) {
        eta = 1 / eta;
        cosTheta_i = -cosTheta_i;
    }
    // 计算 cosTheta_t
    Float sin2Theta_i = 1 - Sqr(cosTheta_i);
    Float sin2Theta_t = sin2Theta_i / Sqr(eta);
    if (sin2Theta_t >= 1)
        return 1.f;
    Float cosTheta_t = SafeSqrt(1 - sin2Theta_t);
 
    Float r_parl = (eta * cosTheta_i - cosTheta_t) /
                   (eta * cosTheta_i + cosTheta_t);
    Float r_perp = (cosTheta_i - eta * cosTheta_t) /
                   (cosTheta_i + eta * cosTheta_t);
    return (Sqr(r_parl) + Sqr(r_perp)) / 2;
}

导体的菲涅尔方程

导体发生反射和折射行为时，它的IOR是一个复数，通常使用实部描述光速的下降，而虚部描述光线在导体内的衰减，光线在导体内的衰减很快，甚至可以影响到反射分量。使用复数并不是IOR真的具有复数的性质，而是将其作为一个数学工具。
光线的振幅在物体中的衰减可以表示为$E(z)=e^{-i\alpha \eta z}$，其中i为虚数单位，$\alpha$为频率，$\eta$为折射率IOR，z为距离。假设现在物体的折射率为依然是一个实数，根据复数三角函数的性质，

$$e^{ix}=cosx+isinx$$

那么函数E可以表示为$E(z)=cos(\alpha \eta z)$。
如果IOR为一个复数$\eta -ik$，其中$\eta$依然表示折射率，k表示衰减程度，那么函数E可以表示为

$$E(z)=e^{-\alpha zk}cos(\alpha \eta z)$$

不论使用哪种表示方式，虚数单位i都是没有使用到的。
使用这种方式来表示菲涅尔方程，具体的实现为

Float FrComplex(Float cosTheta_i, pstd::complex<Float> eta) {
    using Complex = pstd::complex<Float>;
    cosTheta_i = Clamp(cosTheta_i, 0, 1);
    Float sin2Theta_i = 1 - Sqr(cosTheta_i);
    // 由于eta是一个复数，所以计算出来的sin2Theta_t也是一个复数
    Complex sin2Theta_t = sin2Theta_i / Sqr(eta);
    Complex cosTheta_t = pstd::sqrt(1 - sin2Theta_t);
 
    Complex r_parl = (eta * cosTheta_i - cosTheta_t) /
                     (eta * cosTheta_i + cosTheta_t);
    Complex r_perp = (cosTheta_i - eta * cosTheta_t) /
                     (cosTheta_i + eta * cosTheta_t);
    // pstd::norm计算复数的模
    return (pstd::norm(r_parl) + pstd::norm(r_perp)) / 2;
}

为了方便使用，对其进行一个简单的封装，输入eta和k并对其Fr进行评估。

SampledSpectrum FrComplex(Float cosTheta_i, SampledSpectrum eta,
                          SampledSpectrum k) {
    SampledSpectrum result;
    for (int i = 0; i < NSpectrumSamples; ++i)
        result[i] = FrComplex(cosTheta_i,
                              pstd::complex<Float>(eta[i], k[i]));
    return result;
}

粗糙度和微平面理论

现实中物体发生反射时，完美的镜面反射是不存在的，因为没有完美的光滑镜面，物体越粗糙，它的镜面反射就会越弱。
从微观上说，物体的表面是由许多凹凸不平的微平面组成的，光线照射到物体的表面时，这些微平面同时发生反射，物体的表面越光滑（此时微平面之间的法线差异越小，即微平面都朝向同一个方向），整体的反射效果就越强，而物体的表面越粗糙（微平面朝向不同的方向），整体的反射效果就越弱。这就是微平面理论的基础。
按照上面这个理论，其实可以在模型上使用许多细小的三角形来模拟真实的粗糙表面，然后在渲染时对每个微平面来计算反射效果，这样也可以表示出不同的表面粗糙度，但是这对于建模和光线追踪算法来说都是十分困难和低效的，所以通常情况下，会使用统计近似的方法来对微平面理论进行建模。

微平面的法线分布函数

考虑镜面反射和菲涅尔反射原理，几何表面的法线会很大程度影响到物体对光线的反射。然而，就像上面说的，通常不会对物体表面的每个微平面进行建模，而是使用一个法线分布函数来描述所有微平面法线的分布情况，它表示了粗糙度对表面法线的影响。
通常使用$D({\omega }_m)$来表示法线分布函数，参数${\omega }_m$表示微平面的法线。以完美的镜面为例，它的法线分布函数可以表示为：

$$D({\omega }_m)=\delta ({\omega }_m-n)$$

其中n表示宏观平面的法线，${\omega }_m$表示我们想统计的微平面的法线方向。

NOTE

关于$\delta$函数，它在0处为1，在其他地方为0，是一个比较特殊的分布函数

通常情况下，法线分布函数需要满足：

$${\int }_{H^2(n)}D({\omega }_m)({\omega }_m\cdot n)d{\omega }_m={\int }_{H^2(n)}D({\omega }_m)cos{\theta }_{m}d{\omega }_m=1$$

这个公式的物理含义是，给定一个宏观平面，所有微平面沿着宏观平面法线投影后，其投影的面积总和与该宏观平面的面积相等。
还有一个与微平面法线相关的属性就是各向异性，它表示一个物体受到光照影响的效果是否会绕着宏观表面的法线旋转而改变，如果不受此影响，那么这个物体就是各向同性的，反之这个物体就是各向异性的。使用数学的语言来描述，将微平面法线${\omega }_m$表示为球坐标$({\theta }_m,{\varphi }_m)$（法线向量都是归一化的，所以不需要长度参数），如果物体的微平面分布只取决于${\theta }_m$，那么它就是各项同性的，如果同时取决于${\theta }_m$和${\varphi }_m$，那么它就是各向异性的。
由Trowbridge 和 Reitz在1975年提出的法线分布函数是一个使用得比较广泛的函数，它的形式为：

$$D({\omega }_m)=\frac{1}{\pi {\alpha }_x{\alpha }_{y}co{s}^4{\theta }_m(1+ta{n}^2{\theta }_m(\frac{co{s}^2{\varphi }_m}{{\alpha }_x^2}+\frac{si{n}^2{\varphi }_m}{{\alpha }_y^2}){)}^2}$$

其中${\omega }_m=({\theta }_m,{\varphi }_m)$，${\alpha }_x$和${\alpha }_y$表示x方向和y方向上的粗糙度，也决定了物体材质是否各项异性的，当${\alpha }_x={\alpha }_y$时，物体就是各向同性的。
代码实现：

class TrowbridgeReitzDistribution {
  public:
    Float D(Vector3f wm) const {
        Float tan2Theta = Tan2Theta(wm);
        if (IsInf(tan2Theta)) return 0;
        Float cos4Theta = Sqr(Cos2Theta(wm));
        Float e = tan2Theta * (Sqr(CosPhi(wm) / alpha_x) +
                           Sqr(SinPhi(wm) / alpha_y));
        return 1 / (Pi * alpha_x * alpha_y * cos4Theta * Sqr(1 + e));
    }
  private:
    Float alpha_x, alpha_y;
};

通常情况下将法线向量${\omega }_m$变换到法线-切线空间中，在这里物体宏观法线坐标为(0, 0, 1)，这样计算其三角函数值会很方便。

NOTE

这里的向量wm位于法线-切线空间并且是归一化的，所以CosPhi这些函数很容易实现，使用向量坐标与球坐标的相互转换就行

几何遮蔽函数

除了法线分布函数外，微平面的理论还有一个不可忽略的特性—从特定的方向观察，微平面之间会相互阻挡，所有只有一部分微平面是可见的。这是保证BSDF能量守恒的重要条件。
在上面的分析中提到，微平面理论有一个前提，所有微平面在宏观法线上的投影面积与宏观平面相等，然而在现实中，观察的方向与宏观法线的方向往往是不一致的，如下图所示：

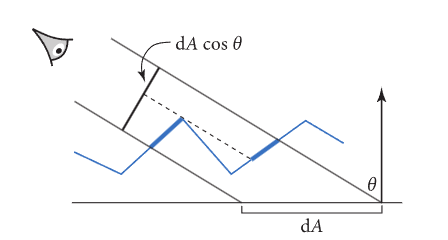
在观察方向上，只有粗线部分是可以被观察到的。
综上所述，微平面理论中还需要一个函数来描述在$\omega$方向上，微平面所被观察到的面积与宏观面积（上图中的$dA$）的比例。这就是几何遮蔽函数$G(\omega ,{\omega }_m)$，$\omega$表示观察方向，${\omega }_m$表示我们想观察的微平面的法线方向。很明显，它满足$0\le G\le 1$。
同时，G和D还满足此条件：

$${\int }_{H^2(n)}D({\omega }_m)G(\omega ,{\omega }_m)max(0,\omega \cdot {\omega }_m)d{\omega }_m=\omega \cdot n=cos\theta$$

然而，业界并未找到符合此条件的G函数，所以采用了一种近似的方法。假设表面上不同点的高度和法线在统计上是独立的（实际上它们是连续的）。这种假设将一个连续的平面看成是悬浮在空间中的许多独立的微平面组成的。这样的话，G函数就与微表面法线${\omega }_m$无关（这里不理解，为什么就无关了），此项就可以从积分中移出，变成下面这个形式，

$$G(\omega ){\int }_{H^2(n)}D({\omega }_m)max(0,\omega \cdot {\omega }_m)d{\omega }_m=cos\theta$$

那么

$$G(\omega )=\frac{cos\theta }{{\int }_{H^2(n)}D({\omega }_m)max(0,\omega \cdot {\omega }_m)d{\omega }_m}$$

这种方法被称为史密斯近似。
将上面的法线分布函数带入此公式后，可以解出$G(\omega )$，通常，他会被写成以下形式，

$$G(\omega )=\frac{1}{1+\Lambda (\omega )}$$

比如，将Trowbridge–Reitz法线分布函数带入公式后解出的结果就是：

$$\Lambda (\omega )=\frac{\sqrt{1+{\alpha }^{2}ta{n}^2\theta }-1}{2}$$

其中$\alpha$为材质粗糙度，如果使用了${\alpha }_x$和${\alpha }_y$来表示粗糙度的话（各项异性材质），$\alpha$可以以下面公式计算：

$$\alpha =\sqrt{{\alpha }_x^{2}co{s}^2\varphi +{\alpha }_y^{2}si{n}^2\varphi }$$

代码实现：

Float G1(Vector3f w) const { return 1 / (1 + Lambda(w)); }
 
Float Lambda(Vector3f w) const {
    Float tan2Theta = Tan2Theta(w);
    if (IsInf(tan2Theta)) return 0;
    Float alpha2 = Sqr(CosPhi(w) * alpha_x) + Sqr(SinPhi(w) * alpha_y);
    return (std::sqrt(1 + alpha2 * tan2Theta) - 1) / 2;
}

阴影-遮蔽函数

几何遮蔽不仅影响了观察方向的光照效果，也会影响入射方向的效果，因为微平面的遮蔽在两个方向上都是存在的。所以完整的遮蔽应该是阴影（入射方向）+遮蔽（观察方向）。
理论上，最终的遮蔽函数应该是两个方向的遮蔽函数相乘，即

$$G({\omega }_o,{\omega }_i)=G({\omega }_o)G({\omega }_i)$$

因为这两个函数在统计上是独立的。然而这样的方式产生的渲染效果并不理想，所以通常会使用如下形式，

$$G({\omega }_o,{\omega }_i)=\frac{1}{1+\Lambda ({\omega }_o)+\Lambda ({\omega }_i)}$$

代码实现：

Float G(Vector3f wo, Vector3f wi) const {
    return 1 / (1 + Lambda(wo) + Lambda(wi));
}

对可见法线进行采样

法线分布函数需要的入参${\omega }_m$需要通过采样获取，既然涉及到采样，就必须计算它的pdf。
PBRT中的是为了追求最高精度的渲染，实际许多渲染器都是直接把入射方向和观察方向的中间向量h当做${\omega }_m$，所以这里单纯了解一下公式，不深入理解了，并且这里理解难度也很大。
Trowbridge–Reitz法线分布函数的分布为：

$$D_{\omega }({\omega }_m)=\frac{G(\omega )}{cos\theta }D({\omega }_m)max(0,\omega \cdot {\omega }_m)$$

代码实现：

Float D(Vector3f w, Vector3f wm) const {
    return G1(w) / AbsCosTheta(w) * D(wm) * AbsDot(w, wm);
}

PDF函数：

Float PDF(Vector3f w, Vector3f wm) const { return D(w, wm); }

采样函数，输入观察方向w和二维随机数u，返回采样的${\omega }_m$方向。

Vector3f Sample_wm(Vector3f w, Point2f u) const {
       // 将w转换为半球结构，方便后面计算
       Vector3f wh =
       Normalize(Vector3f(alpha_x * w.x, alpha_y * w.y, w.z));
       if (wh.z < 0)
           wh = -wh;
 
       // 基于wh构建正交基 
       Vector3f T1 = (wh.z < 0.99999f) ? Normalize(Cross(Vector3f(0, 0, 1), wh))
                                       : Vector3f(1, 0, 0);
       Vector3f T2 = Cross(wh, T1);
 
       // 在圆盘上进行采样
       Point2f p = SampleUniformDiskPolar(u);
 
       // 采样结果投影到半球并重新计算三维坐标
       Float h = std::sqrt(1 - Sqr(p.x));
       p.y = Lerp((1 + wh.z) / 2, h, p.y);
 
       Float pz = std::sqrt(std::max<Float>(0, 1 - LengthSquared(Vector2f(p))));
       Vector3f nh = p.x * T1 + p.y * T2 + pz * wh;
       return Normalize(Vector3f(alpha_x * nh.x, alpha_y * nh.y,
                                 std::max<Float>(1e-6f, nh.z)));
}

采样大概的含义是给定观察方向，获得从该方向可观察到的一个随机法线方向，如下图

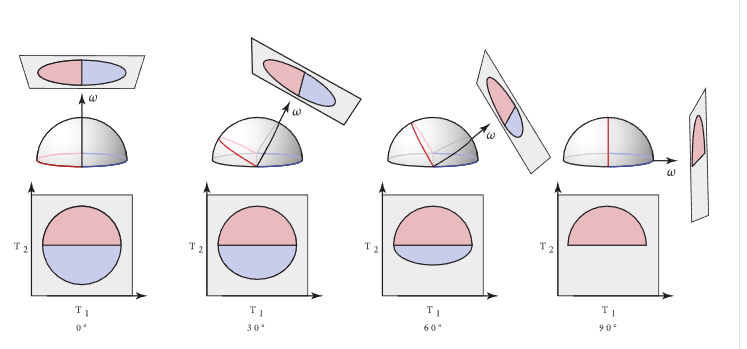
通常是在一个圆盘上进行采样，但是随着观察角度的变化，采样的圆盘会退化成半圆盘。

Torrance–Sparrow模型

总结基于微平面理论的BSDF采样方法，它应该包含三个步骤：

1. 给定观察方向${\omega }_o$，通过上面的对可见法线进行采样方法采样出微平面法线${\omega }_m$，这个步骤包含了光线与微平面相交的过程，相当与采样时选择了法线为${\omega }_m$的微平面。
2. 通过反射定律和菲涅尔方程计算入射方向和反射能量系数。
3. 考虑遮蔽效应，乘以遮蔽函数G以缩放光照能量。
   在实际进行计算时，${\omega }_o$是已知的，${\omega }_m$可以通过上面的可见法线采样来获得，通过镜面反射定律可以求得反射方向（光线追踪算法里是从相机发射光线，与真实世界相反，所以这里是知道了${\omega }_o$来求${\omega }_i$）：

$${\omega }_i=-{\omega }_o+2({\omega }_m\cdot {\omega }_o){\omega }_m$$

反过来考虑，知道了反射方向（观察方向）和入射方向后，就可以求出微平面法线，

$${\omega }_m=\frac{{\omega }_i+{\omega }_o}{||{\omega }_i+{\omega }_o||}$$

其实就是入射和反射方向的半角向量。（这应该就是实时渲染系统中将半角向量h用于微平面法线的原因）。

半角向量

如果将上面3个向量以球坐标表示，并且以${\omega }_r$（上面的${\omega }_o$）作为坐标基础，那么有以下关系，

$${\theta }_i=2{\theta }_m{\varphi }_i={\varphi }_m$$

推导过程如下，在上面的镜面反射定律中，以${\omega }_m$作为坐标基础，根据反射角等于入射角，反射向量与入射向量的关系是：

$${\theta }_r={\theta }_i{\varphi }_r={\varphi }_i+\pi$$

简单解释就是发生反射时，以入射和反射的半角向量做基础，它们的极角是相等的，说明它们与半角向量的夹角相同，方位角相差180度，说明它们分布与半角向量两侧。而当以${\omega }_r$做基础时，入射向量的极角是半角向量的两倍，说明入射向量与反射向量的夹角是半角向量与反射向量夹角的两倍，方位角相等，说明入射向量和半角向量分布在反射向量的同一侧。
为什么需要确定这个关系，如下图：

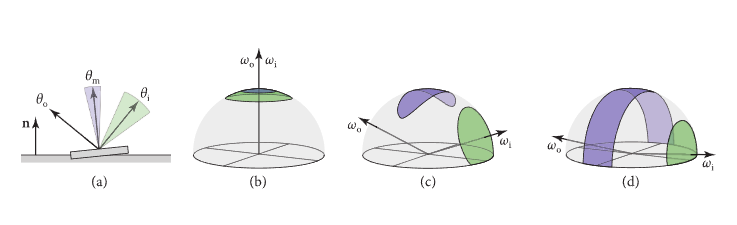
当固定${\omega }_o$并调整${\omega }_i$（绿色部分）时，可以看到形成反射的微表面集合（紫色部分）性状和大小是会发生变化的，这也就意味着，在计算中，随着不同的${\omega }_o$和${\omega }_i$变化，选择的${\omega }_m$的分布会发生变化。
当固定${\omega }_o$时，${\omega }_m$随着${\omega }_i$的变化关系为

$$\begin{array}{rl}\frac{d{\omega }_m}{d{\omega }_i}& =\frac{sin{\theta }_{m}d{\theta }_{m}d{\varphi }_m}{sin{\theta }_{i}d{\theta }_{i}d{\varphi }_i}\\ & =\frac{sin{\theta }_{m}d{\theta }_{m}d{\varphi }_m}{sin2{\theta }_{m}2d{\theta }_{m}d{\varphi }_m}\\ & =\frac{sin\theta }{4cos{\theta }_{m}sin{\theta }_m}\\ & =\frac{1}{4cos{\theta }_m}\\ & =\frac{1}{4({\omega }_i\cdot {\omega }_m)}=\frac{1}{4({\omega }_o\cdot {\omega }_m)}\end{array}$$

关于第一步立体角微分到球坐标微分的转换，在立体角（solid angle）中详细介绍过。

PDF

有了上面半角向量的关系，就可以计算在采样向量${\omega }_i$时其可见法线分布的pdf。

$$p({\omega }_i)=D_{{\omega }_0}({\omega }_m)\frac{d{\omega }_m}{d{\omega }_i}=\frac{D_{{\omega }_0}({\omega }_m)}{4({\omega }_o\cdot {\omega }_m)}$$

Torrance–Sparrow BRDF

根据蒙特卡洛积分和采样的方法，可以得出渲染方程单次采样的计算方式：

$$\begin{array}{rl}{L}_o(p,{\omega }_o)& ={\int }_{H^2(n)}{f}_r(p,{\omega }_o,{\omega }_m)L_i(p,{\omega }_i)cos{\theta }_{i}d{\omega }_i\\ & \approx \frac{f_r(p,{\omega }_o,{\omega }_m)L_i(p,{\omega }_i)cos{\theta }_i}{p({\omega }_i)}\end{array}$$

这里是BRDF，所以只考虑反射，不考虑透射。
按照上面微平面理论的分析，单词采样的值应该考虑菲涅尔定律（计算反射光能量所占比例）、遮蔽函数（计算在微平面的相互遮挡下，还能发生反射的表面积比例）。
按照这个理论，可以得出

$$\frac{f_r(p,{\omega }_o,{\omega }_i)L_i(p,{\omega }_i)cos{\theta }_i}{p({\omega }_i)}=F({\omega }_o,{\omega }_m)G({\omega }_i)L_i(p,{\omega }_i)$$

约去Li并移项，可得

$$f_r(p,{\omega }_o,{\omega }_i)=\frac{p({\omega }_i)F({\omega }_o,{\omega }_m)G({\omega }_i)}{cos{\theta }_i}$$

更据上面通过半角向量计算出的pdf，带入后得

$$f_r(p,{\omega }_o,{\omega }_i)=\frac{D_{{\omega }_o}({\omega }_m)F({\omega }_o,{\omega }_m)G({\omega }_i)}{4({\omega }_o\cdot {\omega }_m)cos{\theta }_i}$$

继续带入上面对可见法线进行采样的$D_{{\omega }_o}({\omega }_m)$,得到

$$f_r(p,{\omega }_o,{\omega }_i)=\frac{D({\omega }_m)F({\omega }_o,{\omega }_m)G({\omega }_i)G({\omega }_o)}{4cos{\theta }_{i}cos{\theta }_o}$$

按照阴影-遮蔽函数的方法将两个遮蔽函数合成一个，得到最终的BRDF

$$f_r(p,{\omega }_o,{\omega }_i)=\frac{D({\omega }_m)F({\omega }_o,{\omega }_m)G({\omega }_i,{\omega }_o)}{4cos{\theta }_{i}cos{\theta }_o}$$

这个BRDF是目前应用得最广泛的反射模型，它并不依赖于特定的微表面分布和菲涅尔函数，可同时用于介质和导体材质。但是它也有一个缺点，在考虑遮蔽效果时，实际上即使光线被遮住了，它依然会继续反射，而这里将被遮住的光线的光照贡献直接视为0，所以整体的光照效果比起现实世界偏暗。