渲染方程

$$L_o(p,{\omega }_o)=L_e(p,{\omega }_o)+{\int }_{\Omega }{f}_r(p,{\omega }_i,{\omega }_o)L_i(p,{\omega }_i)n\cdot {\omega }_{i}d{\omega }_i$$

渲染中在进行光照计算（Shading阶段）时，本质上就是在解这个渲染方程。对这个方程可以先进行一个粗浅的理解：p点反射出的光照强度等于它自身的发光强度加上该点对所有周围光线向${\omega }_o$方向的反射强度总和，这里用积分来表示“周围所有方向的光线”。$f_r(p,{\omega }_i,{\omega }_o)$是BRDF，描述了该点将${\omega }_i$方向入射的光线反射到${\omega }_p$方向的能力，它由物体自身的属性决定。

渲染方程的推导

在理解这个方程是推导过程之前，要先理解一些光学上的概念。

光源的能量

发光的物体总是不断向外辐射出能量，比如太阳、灯泡，在辐射度量学中，这个能量叫做辐射能（radiant energy），一般用Q表示，它的单位是焦耳（J）。

光源的功率

就像物理学上能量和功率的关系一样，光照的功率等于能量除以时间，它描述了单位时间内该光源产生的能量，一般用$\Phi$ 来表示，功率的单位是瓦特（W）。

$$\Phi =\frac{\mathrm{d}Q}{\mathrm{d}t}$$

一个光源的功率越大，说明这个光源发射能量越快。类比到便于理解的距离与速度的关系，速度等于距离除以时间，速度越大，说明这个物体移动越快。
在辐射度量学中，光源的功率也被称为辐射通量或辐射功率（radiant flux/power）。

光通量

光通量是直接描述亮度的物理量，光通量越大，说明光源越亮，光通量的单位是流明（lm表示）。

发光效率

光源的功率并不完全等价于光通量，也就是说并不是一个光源的功率越大，它就越亮。不同的光源有不同的发光效率，发光效率描述了光源将功率转换成亮度的能力，单位是流明每瓦特（lm / W）。
如果知道一个光源的功率和它的发光效率，就可以算出该光源的光通量，也就是亮度。

Note

上面的这些物理量不需要过多考虑，在渲染系统中，光源一般会直接给出亮度（lm），可以直接用于渲染计算。

在渲染方程的推导中依然是以光源的功率（辐射通量）作为光源发光强度的标准，尽管光源的亮度还受到发光效率影响，亮度与功率之间也是一个比较简单的线性变换。

辐照度（Irradiance）

辐照度用于描述物体单位面积内接受的光的能量，它的计算方式为 辐射通量 / 面积，通常用E来表示，

$$E=\frac{\mathrm{d}\Phi }{\mathrm{d}A}$$

辐照度的单位是（$W/m^2$）。
同时，辐照度的计算还遵循Lambert的余弦定理，即单位面积接受的辐射通量与光源入射方向和表面法线的夹角有关，具体的计算方式为

$$E=\frac{\mathrm{d}\Phi }{\mathrm{d}A}cos\theta$$

其中$\theta$为光源入射方向和表面法线的夹角。

Note

关于Lambert的余弦定理，DX12书的光源章节有详细解释。

考虑一个点光源，它均匀地向四周发射能量，那么在它半径为r的球面上的辐照度为

$$E=\frac{\Phi }{4\pi r^2}$$

当r = 1时，球面为一个单位球面，单位球面的辐照度为$\frac{\Phi }{4\pi }$。

辐射强度（Radiant Intensity）

在了解辐射强度的概念前，需要先了解立体角的概念。

立体角（solid angle）

立体角是描述三维空间中一个物体在观察点所占据的空间大小的几何量，类似于二维空间中的角度。

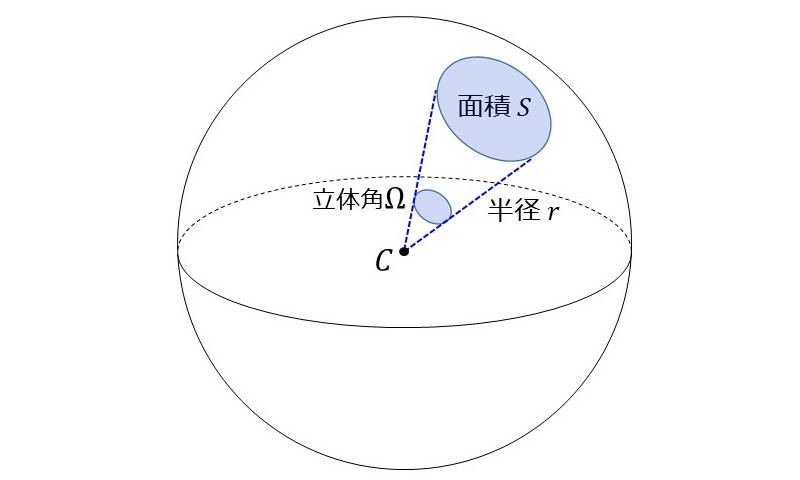
立体角一般使用$\Omega$来表示，它的计算方法为：

$$\Omega =\frac{A}{r^2}$$

其中A表示球面上投影的面积，r表示球的半径。这个计算方式类似于二维空间中弧度制角度的计算，在二维空间中，弧度 = 弧长 / 半径。
立体角的单位为球面度（steradian, sr），$1sr=(180/\pi {)}^2$。一个完整的球面，它的立体角为

$$\Omega =\frac{A}{r^2}=\frac{4\pi r^2}{r^2}=4\pi (sr)$$

同理，一个半球面的立体角为$2\pi (sr)$。

球坐标系：

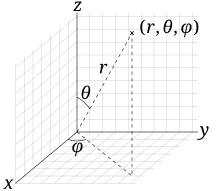
在球坐标系中，一个点$(r,\theta ,\varphi )$处的极小面积$dA=(rsin\theta d\phi )(rd\theta )=r^2(sin\theta d\theta d\phi )$ 。
具体的推导如下：

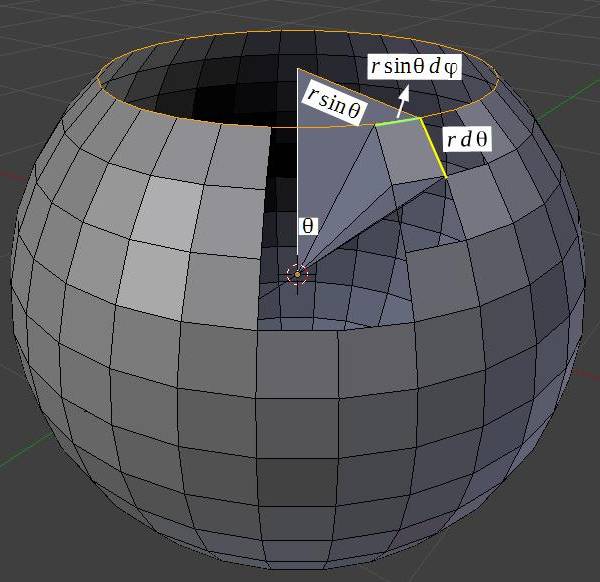
如上图所示，这里将极小面积$dA$看作一个矩形，这个矩形纵向的边（黄色的部分）位于一个半径为r的圆上，知道了它的半径r和角度$d\theta$，很容易计算出它的弧长为$rd\theta$ （使用上面的弧度公式）。矩形的横向边（绿色的部分）位于一个半径为$rsin\theta$的圆上（图中黄色的圆形），它的弧长为$rsin\theta d\phi$，面积即为两段弧长的乘积。
知道了极小面积的表示方法之后，就可以计算极小立体角（或者说微分立体角）,

$$d\omega =\frac{dA}{r^2}=\frac{r^2(sin\theta d\theta d\phi )}{r^2}=sin\theta d\theta d\phi$$

微分立体角可以近似地看作3维空间中某个方向上的一条光线，这对渲染方程的推导很重要。
立体角在球面上的积分：

$$\Omega ={\int }_0^{2\pi }{\int }_0^{\pi }dw={\int }_0^{2\pi }{\int }_0^{\pi }sin\theta d\theta d\phi =4\pi$$

正好就是球的面积。

辐射强度

辐射强度指的是单位立体角内的辐射通量，通常使用I来表示，它的计算公式为 辐射强度 = 辐射通量 / 立体角，$\omega$方向上的辐射强度即为：

$$I=\frac{d\Phi }{d\omega }$$

辐射强度的单位是 瓦特/球面度（W/sr），也称为坎德拉（cd）。
假设一个光源的辐射通量为$\Phi$，它均匀地向每一个方向辐射能量，那么每个方向的辐射强度为

$$I=\frac{\Phi }{4\pi }$$

可以看出辐射强度与半径是无关的，也就是说，在某一个方向上，不论距离多远，光源的辐射强度都是相等的。

辐射率（radiance）

定义为在指定方向上的单位立体角和垂直此方向的单位面积上的辐射通量，通常用L表示。辐射率的单位为瓦特每球面度每平方米（$W/sr\cdot m^2$）,或者称为尼特（nit）。具体的计算公式为

$$L=\frac{d^{{}^{\prime \prime }}\Phi }{dAd\omega cos\theta }$$

这里除以$cos\theta$的原因是：在测量辐射通量时，考虑到Lambert余弦定理，实际的面积是($dA/cos\theta$)，而这里需要的是垂直方向的单位面积，需要将$cos\theta$消除，也就是说需要消除辐射通量测量中平面法线与照射方向不同带来的辐射通量衰减。
辐射率使用来描述一个光源辐射能量的物理量，同时也被称为辐亮度，它不仅考虑了辐射的总量，还精确考虑了辐射的方向性和分布情况。在渲染系统中，光源的辐射率由光源的亮度，方向和颜色来决定。
在渲染一个物体时，本质上是计算该物体向相机（人眼）方向上反射的能量（辐照度），如果把相机考虑成一个点，相机上接受的辐照度就是物体在相机方向的辐射率，所以，辐射率直接决定了一个物体所被观察到的颜色和亮度，或者说相机看到的物体是由物体在相机上的辐射率决定的，渲染时计算该点在相机方向上的辐射率就是在计算该点在相机上的成像结果。

通过周围光源的辐射率计算物体辐照度

假设已经知道了一个光源的辐射率，如何计算某一个点p从该光源接受到的辐照度的大小。
辐射率的定义为在指定方向上的单位立体角和垂直此方向的单位面积上的辐射通量，辐照度的定义为单位面积内接受的光的辐射通量，假设场景中只有一个光源，

$$E(p)=dE(p,\omega )=L(p,w)n\cdot \omega d\omega$$

这从辐射率及辐照度的公式中也可以推出，这里使用$n\cdot \omega$来表示$cos\theta$。
假设场景中有多个光源，那么

$$E(p)=\sum d{E}_i(p,{\omega }_i)=\sum L_i(p,{\omega }_i)n\cdot {\omega }_{i}d{\omega }_i$$

即p点接受的总辐照度为每个光源在p点贡献的辐照度之和。
现在考虑p点接受周围所有光线的照射，包括直接光源和周围物体反射的间接光源，就像现实世界一样，那么辐照度的计算方式就是

$$E(p)={\int }_{\Omega }d{E}_i(p,{\omega }_i)={\int }_{\Omega }{L}_i(p,{\omega }_i)n\cdot {\omega }_{i}d{\omega }_i$$

总辐照度等于周围每个方向上贡献辐照度在半球上的积分，因为背面的光照是不会贡献辐照度的。

通过物体辐照度计算指定方向的辐射率

知道了一个点所受的辐照度之后，就可以反过来计算出这个点在${\omega }_o$方向上的辐射率，也就是计算出这个点在${\omega }_o$方向上的最终成像。
在计算之前，首先要了解一件事，每一种物体的反射能力都是不同，比如镜面，它对光线的反射集中在入射光线方向的反射方向，也就是说当观察点正好在该方向时，可以接收到几乎全部的能量，看到的镜面亮度很亮，而其他方向几乎不能接受到反射的能量，所以镜面经常会出现一个非常集中的“高光”点。而对于布料或者丝绸这类物体来说，它们会将接受的能量向四面八方反射，所以从每个方向观察它们接受到的反射能量都是相似的，所以这类物体的亮度分布非常”均匀“。
即使是同一种物体，对不同波长光线的反射能力也是不同的，如果一个物体只反射红色波长的光，那么它最终就会呈现红色。
看起来，场景中的每个物体对光线的反射能力都不同，计算时需要为每一个物体制定不同的计算公式，这几乎是一件不可能的事情。所以，这里需要引入BRDF的概念。

BRDF

1965年，Fred Nicodemus首次提出BRDF函数的定义：

$$f({\omega }_i,{\omega }_o)=\frac{d{L}_o({\omega }_o)}{d{E}_i({\omega }_i)}$$

BRDF全称为双向反射分布函数（bidirectional reflectance distribution function），一般使用$f({\omega }_i,{\omega }_o)$表示，它定义了一个不透明的物体将从${\omega }_i$方向的入射光线反射到${\omega }_o$方向的能力。比如一个理想的镜面，它将入射光线进行全反射，那么它的BRDF就可以定义为

$$f({\omega }_i,{\omega }_o)=\{\begin{array}{ll}1& {\omega }_o=reflect({\omega }_i,n)\\ 0& otherwise\end{array}$$

其中的reflect函数用于计算一个向量关于法线n的反射向量。上面的BRDF表示此物体将入射光线能量完全反射到反射方向上，而其他方向接受到的能量为0。
满足物理真实性的BRDF有以下几个要求：

1. BRDF永远为一个正数，$f({\omega }_i,{\omega }_o)>=0$
2. BRDF中的光路是可逆的，$f({\omega }_i,{\omega }_o)=f({\omega }_o,{\omega }_i)$
3. 能量守恒，反射光的能量不可能大于入射光能量的总和 ${\int }_{\Omega }f({\omega }_i,{\omega }_o)n\cdot {\omega }_{i}d{\omega }_i<=1$
   有了BRDF，就可以将计算公式统一起来，为每个不同的物体定义它们自己的BRDF，然后用于反射方向辐照度的计算。定义物体的BRDF等价于设置物体的材质，所以在渲染系统中，BRDF = 材质。

Note

尽管BRDF的结果应该是一个0到1之间的数，在真正的渲染应用中，都会将BRDF作为三维的颜色数据来进行计算，也就是BRDF需要同时考虑到物体的基础颜色。

计算指定方向的辐射率

现在，物体的辐照度已经计算完毕了，物体的BRDF也定义好了，那么就可以进行指定的${\omega }_o$方向上的辐射率的计算，同样按照计算周围光线对物体的辐照度的思路，
考虑场景中只有一条入射光线

$$L(p,{\omega }_o)=dL(p,{\omega }_o)=f_r({\omega }_i,{\omega }_o)d{E}_i(p,{\omega }_i)=f_r({\omega }_i,{\omega }_o)L(p,{\omega }_i)n\cdot {\omega }_{i}d{\omega }_i$$

这里使用$f_r$来表示BRDF。
考虑场景中的所有方向的入射光线

$$L(p,{\omega }_o)={\int }_{\Omega }dL(p,{\omega }_o)={\int }_{\Omega }{f}_r({\omega }_i,{\omega }_o)d{E}_i(p,{\omega }_i)={\int }_{\Omega }{f}_r({\omega }_i,{\omega }_o)L(p,{\omega }_i)n\cdot {\omega }_{i}d{\omega }_i$$

再考虑到物体的自发光情况，即物体也能向外辐射能量的情况，最终的辐射率还需要加上物体向${\omega }_o$方向的辐射率。

$$L_o(p,{\omega }_o)=L_e(p,{\omega }_o)+{\int }_{\Omega }{f}_r(p,{\omega }_i,{\omega }_o)L_i(p,{\omega }_i)n\cdot {\omega }_{i}d{\omega }_i$$

如果使用$\theta$和$\phi$来表示$\omega$的话，渲染方程可以写成如下形式：

$$L_o(p,{\theta }_o,{\phi }_o)=L_e(p,{\theta }_o,{\phi }_o)+{\int }_0^{2\pi }{\int }_0^{\pi }{f}_r(p,{\theta }_o,{\phi }_o,{\theta }_i,{\phi }_i)L_i(p,{\theta }_i,{\phi }_i)cos\theta sin\theta d\theta d\phi$$

这里为每个L加了下标以区分它们的含义。
到此为止，渲染方程已经推导完成，总体上来说，渲染方程根据物体周围所有入射光线的辐射率来计算指定出射方向的辐射率，期间还要考虑到物体本身的属性对反射的影响，如果一个物体自身可以发光，那么它自身在出射方向上的辐射率也要考虑进去。

渲染方程的求解

了解了渲染方程的含义之后，接下来需要知道如何解这个方程并写出对应的代码。首先可以观察到，渲染方程的求解难度主要在于积分，所以重点关注方程的积分部分。
在渲染方程中，$L_e,f_r,n,\omega$都是已知的，$\omega$可以以球坐标系来表示，也可以以3维向量来表示，通常将其使用向量表示。

离线渲染

离线渲染对渲染的质量要求高，对性能的要求较低，所以对渲染方程的求解要求尽可能的精确。因为要考虑所有周围的光线，包括了光源的光线和周围物体反射的光线，而周围物体反射光线的辐射率也需要使用渲染方程来计算，所以这是一个递归计算的过程。

一般来说，求一个定积分时，首先要求它的原函数，然后通过牛顿-莱布尼茨公式求解，

$${\int }_a^{b}f(x)dx=F(b)-F(a)$$

在这里，这个方法明显是行不通的，积分项过于复杂，求解不出原函数，所以，这里需要另一种求解积分的方法——蒙特卡洛积分。

蒙特卡洛积分

蒙特卡洛积分是一种使用随机数进行数值积分的方法，可以对定积分进行计算。

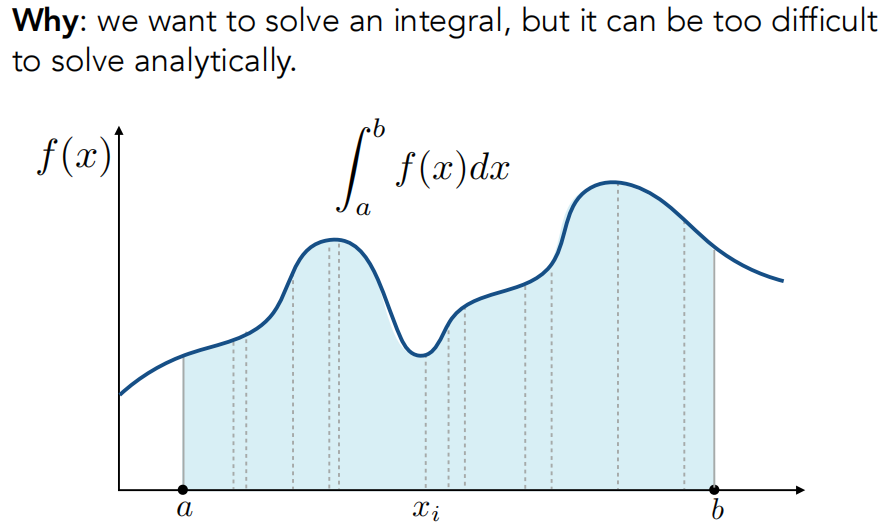
以上图为例，假设想要计算积分

$${\int }_a^{b}f(x)dx$$

显然积分的结果等于上图浅蓝色部分的面积。随机在[a, b]中选择一个点$x_i$，可以计算出它的函数值$f(x_i)$，那么$x_i\cdot f(x_i)$就是积分结果的一个近似值，当然这个近似的误差非常大，但是经过在[a, b]区间内的多次采样，并将每一次的计算结果求平均，就可以得到与积分结果非常近似的一个值。
使用数学公式来表示：

$${\int }_a^{b}f(x)dx=\frac{1}{n}\sum _{i=1}^{n}f(x_i)(b-a)$$

这里的采样是随机在[a, b]中选择的，所以这是一个均匀的采样，它们的概率密度（PDF）为 $1/(b-a)$，可以将上面的公式使用更通用的方法来表示：

$${\int }_a^{b}f(x)dx=\frac{1}{n}\sum _{i=1}^n\frac{f(x_i)}{p(x_i)}$$

其中的$p(x_i)$就表示该采样点的概率密度，类似于每个点的计算结果在最终结果中的“权重”，在这个例子中，每个采样点的“权重”是$1/(b-a)$。
蒙特卡洛积分是一个非常深奥的主题，这里只是非常粗浅地介绍一下，以便于将其用于计算渲染方程。

路径追踪

路径追踪是离线渲染最常用的方法，它的思想是从相机往需要渲染的像素发射光线，光线在场景中弹射，每一次弹射时都需要使用渲染方程计算辐射率，递归计算完成后，就可以得到当前像素的渲染结果。
利用蒙特卡洛积分，可以写出路径追踪的算法（代码来自知乎文章）

float shade(vec3 p, vec3 wo)
{
    float lo = 0.0
    for(int i=0; i < count; i++)
    {
        vec3 wi = random() by pdf;
        ray r = ray(p, wi);
        if(r hit light)
        {
            lo += (1.0 / count) * fr(p, wi, wo) * li * dot(n, wi) / pdf(wi);
        }
        else if(r hit object at o)
        {
            lo += (1.0 / count) * fr(p, wi, wo) * shade(o, -wi) * dot(n, wi) / pdf(wi);
        }
    }
    return lo;
}

在实际应用中，这种方法使用了大量的递归计算，性能很差，一个改进的思路是：每次只弹射一根光线，并且在必要的情况停止它（比如使用俄罗斯轮盘来随机停止，或者到达了最大弹射次数就停止），作为补偿，每一个像素渲染时都需要多次发射光线，最后取平均值来获得精确的结果。
使用这种思想，可以写出改进版的路径追踪算法，这里简单地使用一个概率值来确定是否停止光线（代码来自知乎文章）

float shade(vec3 p, vec3 wo)
{
    float prob = 0.6;// 随便指定一个概率值
    float num = random(0,1);// 随机获取一个0-1的数值
    if(num > prob)
    {
        // 1-prob 的概率不发射光线
        return 0.0;
    }
    vec3 wi = random() by pdf;
    ray r = ray(p, wi);
    if(r hit light)
        return fr(p, wi, wo) * li * dot(n, wi) / pdf(wi) / prob;// 记得要除以发射光线的概率prob
    else if(r hit object at o)
        return fr(p, wi, wo) * shade(o, -wi) * dot(n, wi) / pdf(wi) / prob;
}
 
float generationRay(vec3 camera, vec3 pixel)
{
    float pixel_radiance = 0.0;//初始化像素受到的辐射率
    for(int i=0; i < count; i++)
    {
        vec3 pos = random() by pdf;//根据pdf随机像素内的一个位置
        ray r = ray(camera, pos-camera);//从相机往pos发射射线
        if(r hit object at p)//如果射线打到物体上，交点为p
        {
            //利用shade计算p点camera方向的radiance
            pixel_radiance += (1 / count) * shade(p, camera-pos);
        }
    }
    return pixel_radiance;
}

实时渲染

实时渲染对性能的要求很高，为了性能可以牺牲渲染的质量，对渲染方程的求解也以近似为主，不会对精确度有很高要求。
在实时渲染中，将渲染方程的积分近似为求和，

$${\int }_{\Omega }{f}_r(p,{\omega }_i,{\omega }_o)L_i(p,{\omega }_i)n\cdot {\omega }_{i}d{\omega }_i=\sum _{i=0}^n{f}_r(p,{\omega }_i,{\omega }_o)L_i(p,{\omega }_i)n\cdot {\omega }_i$$

这是一个非常粗略的近似，将积分近似为求和表示只考虑直接光源，忽略的那些物体反射过来的光线，所以实时渲染如果想实现全局光照的话，需要用其他技术来弥补。
实时渲染的着色算法实现：

float shade(vec3 p, vec3 wo)
{
    float lo = 0;
    
    for (light in scene)
    {
        vec3 wi = light.pos - p;
        lo += fr(p, wi, wo) * light.li * dot(n, wi);
    }
    
    return lo;
}

与离线渲染相比，实时渲染的算法非常简单，效率也高出很多。

Reference

# 路径追踪（Path Tracing）与渲染方程(Render Equation)