透视投影矩阵详解

关于透视投影矩阵的推导，网络上已经有了大量的推导教程，但是各种思路层出不穷，有的使用fov和宽高比r已经远近平面来表示视锥体，有的使用进平面的4个边加上远近平面来表示视锥体，有的把NDC空间表示为$[-1,1{]}^3$，有的需要把z值规范到$[0,1]$之中，导致推导出的矩阵五花八门，这里认真梳理一下投影矩阵的推导过程。
基础的一些概念直接省略。

使用fov和宽高比来表示视锥体

假设将一个视锥体表示为垂直视场角 $\theta$，宽高比r，进平面n，远平面f 4个参数，并且z值的规范坐标为$[0,1]$，那么它的透视投影矩阵推导如下：

DX12书的思路

先考虑x和y两个坐标，根据相似三角形的原理，将一个点(x, y, z)投影到近平面上，得到的新坐标为：

$$\begin{array}{r}\frac{x^{\prime }}{n}=\frac{x}{z}=>x^{\prime }=\frac{n}{z}x\\ \frac{y^{\prime }}{n}=\frac{y}{z}=>y^{\prime }=\frac{n}{z}y\end{array}$$

上面的式子中n, x, y, z都是已知的，所以可以直接求出$x^{\prime }$和$y’$。
但是为了方便计算，需要将投影后的坐标规范化，上面未规范化的坐标我们将其称为投影空间或者裁剪空间坐标，规范化后的坐标称为NDC空间坐标，NDC空间的坐标才是在渲染流水线中使用的。
接下来将x和y规范化，因为使用的是垂直视场角$\theta$，先来考虑纵坐标。
首先根据垂直视场角的定义，假设视锥体的高度为h，则

$$\frac{h}{2}=n\ast tan(\frac{\theta }{2})$$

投影后的纵坐标满足

$$-\frac{h}{2}\le y^{\prime }\le \frac{h}{2}$$

想要把它规范化到$[-1,1]$，需要将y除以$\frac{h}{2}$，正好上面已经使用n和$\theta$表示出来了，于是

$$y_{ndc}=y^{\prime }/\frac{h}{2}=\frac{y}{ztan(\theta /2)}$$

同理，虽然没有使用水平视场角，但是通过宽高比$r=width/height$。可以得到

$$\frac{w}{2}=r\ast n\ast tan(\frac{\theta }{2})$$

所以也可以得到

$$x_{ndc}=x^{\prime }/\frac{w}{2}=\frac{x}{rztan(\theta /2)}$$

接下来考虑最为复杂的z坐标，z坐标不只是简单的投影，从上面的x和y坐标可以看出，投影x和y时是与该点的z坐标相关联的，然而推导除的投影矩阵肯定是不能包含z变量的。
这时就需要将其分为线性与非线性两个部分来考虑，线性部分为除以z，使用齐次坐标来实现，具体来说就是将齐次坐标w设置为z，后面进行齐次除法的时候就可以进行除以z运算了，而z坐标的变换是一个Ax+B类型的变换。（书上这里的介绍并不清晰，齐次坐标的部分解释了，但为什么z是一个Ax+B类型的变换没有解释清楚）
这样就得到了投影矩阵的形式：

$$\left|\begin{array}{ccccccc}\frac{1}{rtan(\theta /2)}& & 0& & 0& & 0\\ 0& & \frac{1}{tan(\theta /2)}& & 0& & 0\\ 0& & 0& & A& & 1\\ 0& & 0& & B& & 0\end{array}\right|$$

将坐标与此矩阵相乘:

$$[x,y,z,1]\left|\begin{array}{ccccccc}\frac{1}{rtan(\theta /2)}& & 0& & 0& & 0\\ 0& & \frac{1}{tan(\theta /2)}& & 0& & 0\\ 0& & 0& & A& & 1\\ 0& & 0& & B& & 0\end{array}\right|=[\frac{x}{rtan(\theta /2)},\frac{y}{tan(\theta /2)},Az+B,z]$$

进行齐次除法得到

$$[\frac{x}{rztan(\theta /2)},\frac{y}{ztan(\theta /2)},A+B/z,1]$$

现在将z归一化到$[0,1]$,则有

$$\{\begin{array}{llc}A+B/z=0& & z=n\\ A+B/z=1& & z=f\end{array}$$

解得

$$\begin{array}{r}A=\frac{f}{f-n}\\ B=\frac{-nf}{f-n}\end{array}$$

所以最终得投影矩阵为

$$\left|\begin{array}{ccccccc}\frac{1}{rtan(\theta /2)}& & 0& & 0& & 0\\ 0& & \frac{1}{tan(\theta /2)}& & 0& & 0\\ 0& & 0& & \frac{f}{f-n}& & 1\\ 0& & 0& & \frac{-nf}{f-n}& & 0\end{array}\right|$$

计算机图形学基础书的思路

先假设只进行正交投影，那么投影直接将点的坐标归一化到NDC空间之中，为了方便，先将视锥体近平面的宽度设置为w，高度设置为h，那么将坐标归一化只需要进行一个缩放操作和一个平移操作。
由于缩放是基于原点的，所以矩阵必须先将视锥体的原点（近平面中心）平移到原点（0， 0， 0）处，那么平移矩阵为：

$$M_t=\left|\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& -n& 1\end{array}\right|$$

再考虑缩放，很容易可以得到，

$$\begin{array}{rl}{x}^{\prime }& =\frac{1-(-1)}{w}x=\frac{2}{w}x\\ y^{\prime }& =\frac{2}{h}y\\ z^{\prime }& =\frac{1}{f-n}z\end{array}$$

这里由于NDC空间中x和y的范围是$[-1,1]$，而z的范围是$[0,1]$，所以它的分子为1。
那么缩放矩阵为

$$M_s=\left|\begin{array}{cccc}\frac{2}{w}& 0& 0& 0\\ 0& \frac{2}{h}& 0& 0\\ 0& 0& \frac{1}{f-n}& 0\\ 0& 0& 0& 1\end{array}\right|$$

最终的正交投影为：

$$M_{orth}=M_t\ast M_s=\left|\begin{array}{cccc}\frac{2}{w}& 0& 0& 0\\ 0& \frac{2}{h}& 0& 0\\ 0& 0& \frac{1}{f-n}& 0\\ 0& 0& \frac{-n}{f-n}& 1\end{array}\right|$$

现在再来考虑透视投影，透视投影比正交投影多一个步骤，那就是在进行正交投影之前，需要将坐标按照深度值进行缩放，具体的缩放规则上面已经推导出了，对于x和y坐标，

$$\begin{array}{r}{x}^{\prime }=\frac{n}{z}x\\ y^{\prime }=\frac{n}{z}y\end{array}$$

注意这里不再需要将它们归一化了，因为这个操作将在后面的正交投影中进行。
与上面同样的思路，推导出的矩阵中肯定是不能含z坐标的，所以借助齐次坐标来进行除z操作，那么可以得出这个特殊缩放矩阵的部分数据，

$$M_{press}=\left|\begin{array}{cccc}n& 0& 0& 0\\ 0& n& 0& 0\\ 0& 0& A& 1\\ 0& 0& B& 0\end{array}\right|$$

这里书上依然没有清楚地解释为什么z的变换时Az+B的形式，在Games101中，是通过穷举法来确定它就是这个形式的。。。。
同样根据Az+B这个形式推导A和B，执行齐次除法后，有

$$\begin{array}{r}A+B/n=n\\ A+B/f=f\end{array}$$

透视投影的原则，近平面上的点和远平面上的点投影前后z值不变，同样，这里不需要将其考虑归一化，下一步的正交投影会完成这个工作，
解出A和B

$$\begin{array}{rl}A& =n+f\\ B& =-nf\end{array}$$

所以$M_{press}$的最终形式为：

$$M_{press}=\left|\begin{array}{cccc}n& 0& 0& 0\\ 0& n& 0& 0\\ 0& 0& n+f& 1\\ 0& 0& -nf& 0\end{array}\right|$$

接下来就可以计算最终的投影矩阵：

$$M_{proj}=M_{press}\ast M_{orth}=\left|\begin{array}{cccc}\frac{2n}{w}& 0& 0& 0\\ 0& \frac{2n}{h}& 0& 0\\ 0& 0& \frac{f}{f-n}& 1\\ 0& 0& \frac{-nf}{f-n}& 0\end{array}\right|$$

然后将w和h用r和$\theta$来表示，

$$\begin{array}{rl}h& =2ntan(\frac{\theta }{2})\\ w& =2rntan(\frac{\theta }{2})\end{array}$$

最终的投影矩阵为

$$M_{proj}==\left|\begin{array}{cccc}\frac{1}{rtan(\frac{\theta }{2})}& 0& 0& 0\\ 0& \frac{1}{tan(\frac{\theta }{2})}& 0& 0\\ 0& 0& \frac{f}{f-n}& 1\\ 0& 0& \frac{-nf}{f-n}& 0\end{array}\right|$$

与上面推导出的投影矩阵相同。

总结

投影矩阵的推导重点在以下几个方面：

1. 使用齐次坐标来实现除z的操作，这样就可以将投影时x和y的坐标与z坐标的值关联起来。
2. 投影后的坐标要位于NDC空间之中，这一步用投影后坐标的齐次除法来实现。
3. 投影时位于进平面和远平面上的点投影前后z值不变，这个性质可以用来推导z坐标的变换规则。

使用近平面的四条边和远近两个平面来表示视锥体

这是另一种视锥体的表示方式，使用近平面的四条边l, r, b, t（也可以看作进平面的左下和右上两个顶点）和远近平面n，f来表示。尽管表示方法不一样，但是透视投影矩阵推导的思路是一样的，这里直接沿用上面的结论，将矩阵使用另一种方式来表示。
可以看出，两种表示方式有以下转换关系：

$$\begin{array}{r}t-b=h=2ntan(\frac{\theta }{2})=>tan(\frac{\theta }{2})=\frac{t-b}{2n}\\ r-l=w=2rntan(\frac{\theta }{2})=>rtan(\frac{\theta }{2})=\frac{r-l}{2n}\end{array}$$

所以使用这种方式表示的矩阵为：

$$M_{proj}==\left|\begin{array}{cccc}\frac{2n}{r-l}& 0& 0& 0\\ 0& \frac{2n}{t-b}& 0& 0\\ 0& 0& \frac{f}{f-n}& 1\\ 0& 0& \frac{-nf}{f-n}& 0\end{array}\right|$$

假设将z归一化到[1,-1]区间

上面的推导都是将z坐标，即深度值归一化到$[0,1]$区间，这符合现代图形学API（DX12和vulkan）中的用法，而在某些其他API中，比如opengl，其深度值区间为$[1,-1]$。因为使用右手坐标系的话，在摄像机视角中，当x轴向右，y轴向上是，-z轴是沿着相机的观察方向的，所以将其表示为$[1,-1]$。
投影矩阵依然使用之前的推导思路，其中x和y坐标是不用变的，只是z坐标的变换需要推导，现在已经得到了以下矩阵：

$$\left|\begin{array}{ccccccc}\frac{1}{rtan(\theta /2)}& & 0& & 0& & 0\\ 0& & \frac{1}{tan(\theta /2)}& & 0& & 0\\ 0& & 0& & A& & 1\\ 0& & 0& & B& & 0\end{array}\right|$$

同样按照上面的方法，现在有：

$$\{\begin{array}{l}A+B/n=1\\ A+B/f=-1\end{array}$$

可以得到：

$$\begin{array}{r}A=-\frac{f+n}{f-n}\\ B=\frac{2nf}{f-n}\end{array}$$

所以最终的投影矩阵为：

$$M_{proj}==\left|\begin{array}{ccccccc}\frac{1}{rtan(\theta /2)}& & 0& & 0& & 0\\ 0& & \frac{1}{tan(\theta /2)}& & 0& & 0\\ 0& & 0& & -\frac{f+n}{f-n}& & 1\\ 0& & 0& & \frac{2nf}{f-n}& & 0\end{array}\right|$$

不规则的视锥体

在上面的推导中，都是假设视锥体的正中心位于z轴上，还有一种特殊情况，那就是视锥体中心偏离了相机的z轴，如下图，

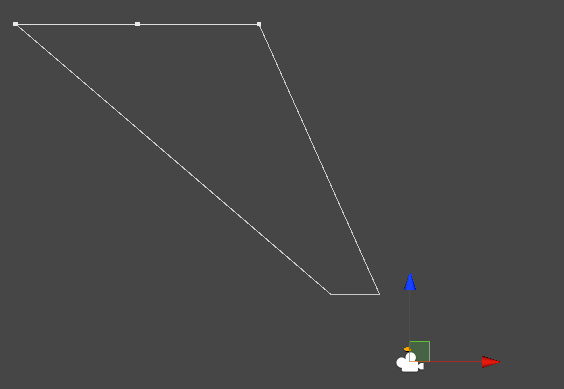
这就是视锥体向-x方向偏移的示意图，这个相机的功能一般称为x-shift或者y-shift。那么使用这种类型的视锥体的时候，投影矩阵又是什么样的呢？
可以看到，即使使用了这种类型的视锥体，它也只是影响了x和y坐标的计算，对于z坐标是没有任何影响的，并且，投影中相似三角形的规则依然可以使用，所以它其实只是影响了x和y轴归一化的计算规则。在之前的推导中，由于视锥体中心位于z轴上，对x和y的归一化可以直接使用一个缩放变换完成，但现在明显不行，应该在缩放之前先增加一个平移的变换将视锥体近平面变换到相机原点。
现在继续来推导这个变换矩阵，假设以x-shift和y-shift来表示视锥体的偏移量，对于x和y投影，依然是，

$$x^{\prime }=\frac{n}{z}x$$ $$y^{\prime }=\frac{n}{z}y$$

但对它们的归一化不再是除以$\frac{w}{2}$和$\frac{h}{2}$那么简单，而是要多一个平移变换，

$$M_{ndc}=\left|\begin{array}{ccccc}1& & 0& & 0\\ 0& & 1& & 0\\ -x_{shift}& & -y_{shift}& & 1\end{array}\right|\ast \left|\begin{array}{ccccc}\frac{2}{w}& & 0& & 0\\ 0& & \frac{2}{h}& & 0\\ 0& & 0& & 1\end{array}\right|=\left|\begin{array}{ccccc}\frac{2}{w}& & 0& & 0\\ 0& & \frac{2}{h}& & 0\\ -x_{shift}\frac{2}{w}& & -y_{shift}\frac{2}{h}& & 1\end{array}\right|$$

可以看出x和y坐标进行归一化是一个平移加缩放的变换，具体的关系为：

$$\begin{array}{r}{x}_{ndc}=x^{\prime }\frac{2}{w}-x_{shift}\frac{2}{w}\\ y_{ndc}=y^{\prime }\frac{2}{h}-y_{shift}\frac{2}{h}\end{array}$$

与上面投影的部分结合，可以得到透视投影矩阵中的x和y变换的部分

$$M=\left|\begin{array}{ccccc}x\frac{n}{z}\frac{2}{w}& & 0& & 0\\ 0& & y\frac{n}{z}\frac{2}{h}& & 0\\ -x_{shift}\frac{2}{w}& & -y_{shift}\frac{2}{h}& & 1\end{array}\right|$$

同样根据w,h和r, $\theta$的关系，并且使用齐次除法的方式先忽略z变量，得到的矩阵为

$$M=\left|\begin{array}{ccccc}\frac{1}{rtan(\theta /2)}& & 0& & 0\\ 0& & \frac{1}{\tan (\theta /2)}& & 0\\ -x_{shift}\frac{1}{rntan(\theta /2)}& & -y_{shift}\frac{1}{ntan(\theta /2)}& & 1\end{array}\right|$$

补充其他部分，可以得到最终的投影矩阵

$$M_{proj}=\left|\begin{array}{ccccccc}\frac{1}{rtan(\theta /2)}& & 0& & 0& & 0\\ 0& & \frac{1}{tan(\theta /2)}& & 0& & 0\\ -x_{shift}\frac{1}{rntan(\theta /2)}& & -y_{shift}\frac{1}{ntan(\theta /2)}& & \frac{f}{f-n}& & 1\\ 0& & 0& & \frac{-nf}{f-n}& & 0\end{array}\right|$$

这里x和y平移的部分不是放在第4行（3维坐标的平移部分），因为透视投影是需要做齐次除法的，放在第四行的元素最终有一个除以z的计算，并不是我们需要的，放在第3行的元素会将z坐标乘在上面，后面再除以z就不影响了。也可以理解成这里的偏移变换并不涉及z坐标，它其实是2维中的平移变换，所以放在第三行。
同样，也可以使用r, l, t, b, f, n的方式来表示视锥体，使用这种方式表示的话，就不需要x-shift和y-shift了，因为r, l, t, b已经可以直接表示中心不在z轴上的进平面了，x-shift和y-shift可以通过它们计算出来，

$$\begin{array}{r}{x}_{shift}=\frac{r+l}{2}\\ y_{shift}=\frac{t+b}{2}\end{array}$$

同样根据之前的转换关系

$$\begin{array}{r}tan(\frac{\theta }{2})=\frac{t-b}{2n}\\ rtan(\frac{\theta }{2})=\frac{r-l}{2n}\end{array}$$

得到投影矩阵

$$M_{proj}==\left|\begin{array}{cccc}\frac{2n}{r-l}& 0& 0& 0\\ 0& \frac{2n}{t-b}& 0& 0\\ \frac{r+l}{l-r}& \frac{t+b}{b-t}& \frac{f}{f-n}& 1\\ 0& 0& \frac{-nf}{f-n}& 0\end{array}\right|$$