背景

在渲染中，积分的计算非常普遍。最基础的渲染方程就是一个积分公式，其他的如相机传感器响应，材质次表面散射等渲染功能也涉及到积分计算，所以计算积分的算法设计在渲染系统中非常重要。
通常情况下计算积分时会想到使用解析法，即求解被积函数的原函数，然后使用牛顿-莱布尼茨公式求解，然而这种方法在渲染系统中是行不通的，渲染中计算的积分函数非常复杂，无法求解出原函数，并且一般会涉及到二维甚至三维的积分，所以解析法难以在渲染系统中实现。
另一种计算积分的方法是数值法，也就是蒙特卡洛积分，通过对数值的估计求解积分的近似解，只要求出被积函数f(x)在某个点x0的取值f(x0)，就可以通过多次采样再求平均的方法来求出积分的解，并且这种方法可以也用于多维积分，这样就解决了渲染中求解积分困难的问题。

蒙特卡洛积分的基础

蒙特卡洛积分是一种基于随机数的方法，需要一些概率与统计的基础知识，所以在了解蒙特卡洛积分之前，先了解一些相关的背景知识。

随机变量和概率

随机变量指的是通过某些方法随机选取的一个值，通常使用X来表示，随机变量可以是离散的，也可以是连续的。通常随机变量都有着定义域，比如随机选择一个实数，它的定义域就为R。

关于离散型的随机变量，以最常见的掷骰子为例，以X来表示掷出的点数，则 $X_{i} \in {1, 2, 3, 4, 5, 6}$ 。以p来表示每个点数掷出的概率，则 $p (X_{i}) = \frac{1}{6}$ ，这表示掷出每一个点数的概率都是1/6，明显可以看出，掷出所有点数的概率相加为1。用来给出离散随机变量的概率的函数称为概率质量函数 (PMF)，通常使用p来表示，在掷骰子这个例子中， $p (X) = \frac{1}{6}$ 。

连续型随机变量与离散型不同，它的取值有无穷多个，并且充满整个定义域。比如在[0, 2]中随机选择一个实数 $X_{i}$ ，就无法直观地看出这个数的具体概率 $p (X_{i})$ （事实上连续型随机变量取到特定值的概率为0，但它并不是一个不可能事件，一般研究连续型随机变量的时候都是研究取到某个区间的概率）。在渲染系统中，比如向半球面的随机一个方向投射光线，该方向就是一个离散型的随机变量。

一种比较特殊的随机变量叫做规范均匀随机变量（canonical uniform random variable），这种随机变量相互独立，并且在其定义域上以均匀的概率取值，掷骰子和掷硬币就是典型的规范均匀随机变量。这种随机变量在程序设计中经常应用，因为很多库都提供了在运行时的随机数生成器。

累积分布函数 cumulative distribution function (CDF) P(x)描述了随机变量X小于或等于x的概率，即

P (x) = p (X \leq x)

比如在掷骰子的例子中，P(2) = 1/3，因为点数小于等于2的可能性有两种：1和2，出现的概率为2/6。在离散型随机变量中， $P (x) = \sum_{j = 1}^{x} p_{j}$ ，在连续型随机变量中， $P (x) = \int_{- \infty}^{x} p df (t) d t$ 。

概率密度函数 probability density function (PDF)描述了一个连续型随机变量取到某个特定值的概率，与离散型随机变量的PMF类似。PDF的定义是CDF的导数。即

p df (x) = \frac{d P ( x )}{d x}

pdf是一个非负数，并且在随机变量定义域内的积分等于1，对于给定区间[a, b]来说，随机变量 $x \in [a, b]$ 的概率为：

p (a \leq x \leq b) = P (b) - P (a) = \int_{a}^{b} p df (x) d x

对于均匀分布的连续型随机变量来说，它的pdf是一个常数。假设随机变量x在[a, b]上连续均匀分布，那么它的pdf为：

p df (x) = {\frac{1}{b - a} 0 (a \leq x \leq b) e l se w h ere

假设在一个单位球体的表面均匀采样，比如从一个点选定某一个方向向四周发射光线，那么这些样本的pdf就为 $\frac{1}{4 π}$ ， $4 π$ 为球体的表面积。

数学期望

在概率论和统计学中，一个离散性随机变量的数学期望是试验中每次可能的结果乘以其结果概率的总和。换句话说，期望像是随机试验在同样的机会下重复多次，所有那些可能状态平均的结果，便基本上等同“期望”所期望的数。数学期望通常也称为加权平均数，通常使用E来表示。

E (f (x)) = i = 1 \sum n f (x_{i}) p (x_{i})

对于连续型随机变量来说，数学期望的定义是随机变量x在其分布函数f(x)定义域上的平均值，，

E (f (x)) = \int_{D} f (x) p (x) d x

其中p(x)表示x的pdf。
假设一个随机变量x在 $[0, π]$ 上的分布函数是 $cos x$ ，并且它是均匀分布的，即 $p df (x) = \frac{1}{π - 0}$ ，那么它的数学期望为：

E (cos x) = \int_{0}^{π} \frac{cos x}{π} d x = \frac{1}{π} (s inπ - s in 0) = 0

数学期望有两个重要的性质，

假设a为常数，则 $E (a f (x)) = a E (f (x))$
多个变量之和的数学期望等于每个变量的数学期望之和 $E (i = 1 \sum n f (X_{i})) = i = 1 \sum n E (f (X_{i}))$

蒙特卡洛估计器

定义一个蒙特卡洛估计器（Monte Carlo estimator）来近似一个积分的值。
假设需要计算一维积分 $\int_{a}^{b} f (x) d x$ 的值，给定一个独立均匀的随机变量 $X_{i} \in [a, b]$ ，那么蒙特卡洛估计器的定义为:

F_{n} = \frac{b - a}{n} i = 1 \sum n f (X_{i})

则它的数学期望 $E (F n)$ 近似于积分的值。
证明其正确性：

E (F n) = E (\frac{b - a}{n} i = 1 \sum n f (X_{i})) = \frac{b - a}{n} i = 1 \sum n E (f (X_{i})) = \frac{b - a}{n} i = 1 \sum n \int_{a}^{b} f (x) p (x) d x = \frac{b - a}{n} i = 1 \sum n \int_{a}^{b} f (x) \frac{1}{b - a} d x = \frac{1}{n} i = 1 \sum n \int_{a}^{b} f (x) d x = \int_{a}^{b} f (x) d x

这里用到了数学期望的两个性质，并且由于随机变量 $X_{i}$ 是独立均匀分布的，所以它的pdf正好可以和外面的 $b - a$ 消掉。在这个证明的过程中有一步将 $E (f (X_{i}))$ 替换成了 $\int_{a}^{b} f (x) p (x) d x$ ，这一步是遵循了大数定律，即样本均值会随着样本数量的增加而收敛于真实的数学期望。只有在样本数量足够多时，这个结论才成立，所以蒙特卡洛估计器是有误差的，并且这个误差随着样本的增加而减小。
虽然这里说的是数学期望 $E (F n)$ 近似于积分的值，但是需要注意的是 $F_{n}$ 本身就是一个对采样点求平均值的过程，所以在样本数够多的情况下， $F_{n} = E (F_{n})$ ，所以只需要计算 $F_{n}$ 就可以估计积分的值了。 Doubtful 这里的理解还不够深入

这个结论可以扩展到多维的积分计算，比如想要计算二维积分 $\int_{y_{0}}^{y_{1}} \int_{x_{0}}^{x_{1}} f (x) d x d y$ 的值，它的蒙特卡洛估计器就为：

F_{n} = \frac{( y _{1} - y _{0} ) ( x _{1} - x _{0} )}{n} i = 1 \sum n f (X_{i})

其中随机变量 $X_{i} = (x_{i}, y_{i}) \in [x_{0}, x_{1}] \times [y_{0}, y_{1}]$ 是独立且均匀分布的。
更通用的，假设选取的随机变量 $X_{i}$ 并不是独立均匀分布的，它的pdf函数为 $p (x)$ ，则它的蒙特卡洛估计器定义为:

F_{n} = \frac{1}{n} i = 1 \sum n \frac{f ( X _{i} )}{p ( X _{i} )}

证明它的数学期望等于 $f (x_{i})$ 积分的过程与上面独立均匀随机变量相似。
使用这个方法求解积分的优势就是可以在计算多维的积分时在多个维度任意选择样本，不用过多考虑积分的维数对计算的影响。比如计算二维积分时可以直接在x和y上采样一个二维点，而不用考虑x和y的计算顺序这些问题。

蒙特卡洛估计器的误差

在统计学中，通常使用方差来衡量统计结果与期望值的偏差。这里同样用方差来衡量蒙特卡洛估计器的误差，并且方差在评估该算法的收敛性能上也有帮助。
方差的定义为：

V [F] = E [(F - E [F])^{2}]

由于方差有以下性质：

V [a F] = a^{2} V [F]

其中a为常数。结合上面数学期望的性质，可以将方差用以下形式来表示：

V [F] = E [F^{2}] - E [F]^{2}

即方差等于采样数平方的期望减去期望的平方。
同样，多个随机变量的方差也有以下性质：

V [i = 1 \sum n X_{i}] = i = 1 \sum n V [X_{i}]

在蒙特卡洛估计器中，方差随着采样数量的增加而减小，假设n为采样的数量，则方差的减小速率为 $O (n^{\frac{1}{2}})$ 。它的好处就是不论采样的维数如何增加，它的方差减小速率是恒定的，这在计算多维积分时很有优势。这个性质导致在使用这种方法进行图像渲染时，最开始的采样点可以很快地提升渲染质量，而当采样点数变得很多时，每增加一个采样点，渲染质量的提升会变得很不明显。

可以使用方差来估算蒙特卡洛估计器的效率，假设一个蒙特卡洛估计器的方差为 $V [F]$ ，而它运行消耗的时间为 $T [F]$ ，那么它的效率为:

ϵ = \frac{1}{V [ F ] \cdot T [ F ]}

方差越小，消耗时间越短，这个蒙特卡洛估计器效率就越高。

并不是所有估计器的期望值都等于积分的值（假设采样数量足够大），这种估计器叫做有偏估计器（biased estimator），与之相对的如果估计器的期望值等于积分的值，那么此估计其叫做有偏估计器（unbiased estimator）。看起来无偏估计器总是比有偏估计器更好，实施却并非如此，除了精度之外，估计器也要考虑效率问题，如果一个有偏估计器的效率很高，那么它可以将节省的时间用来进行更多的采样，以此弥补精度不足的问题。
在渲染中，使用的蒙特卡洛估计器大都是无偏的。

提升采样效率

前面已经提到，使用蒙特卡洛估计器时，方差随着采数量的增加而减少，假设渲染出的图片噪点太多，可以使用更多采样来减少噪点。然而有时渲染有性能要求，采样的数量必须被限制在一个范围内，防止渲染时消耗过多的时间，这时就要从另一个角度考虑，在不提升采样数量的情况下，让采样的效率更高。就比如如果一个函数定义域为 $[0, 2]$ ，但是它在 $[0, 1]$ 内的值非常接近于0，而在 $[1, 2]$ 上的值很大，那么在样本数有限的情况下，将采样的区间放到 $[1, 2]$ 内会更有效果。

分层抽样

分层抽样的思想是将积分的定义域分解成多个区域，然后在每个区域中放置样本。对像素的超采样就是使用了这种方法，将一个像素的区域分解成 $k \times k$ 个小区域，并在其中进行采样，与直接生成像素点内的 $(x, y)$ 坐标的方式相比，分层采样可以保证样本在像素内的分布是尽量均匀的，不会出现多个样本聚集在一起的情况，这也就保证了采样误差的减少。
下面详细分析分层抽样对方差的影响。
分层抽样将积分的定义域 $\land$ 分解成了多个区域 $\land_{1}, \land_{2}, ..., \land_{n}$ ，每一个区域叫做层（stratum），所有层合并起来等于原始的定以域：

i = 1 ⋃ n \land_{i} = \land

使用 $n_{i}$ 表示第i层的采样数量， $p_{i}$ 表示第i层的概率密度，那第i层的蒙特卡洛估计就为:

F_{i} = \frac{1}{n _{i}} j = 1 \sum n_{i} \frac{f ( X ( i , j )}{p _{i} ( X ( i , j ))}

其中 $X (i, j)$ 指的是第i层的第j个样本，如果使用 $v_{i}$ 来表示每一层的权重（如果是均匀地分层，那么所有层的权重均为 $1/ n$ ），最终整个积分的蒙特卡洛估计器为：

F = i = 1 \sum n v_{i} F_{i}

假设第i层的真实积分值为：

μ_{i} = \frac{1}{v _{i}} \int_{\land_{i}} f (x) d x

那么第i层的误差为：

σ_{i}^{2} = E [(F - E [F])^{2}] = E [(F_{i} - μ_{i})^{2}] = \frac{1}{v _{i}} \int_{\land_{i}} (f (x) - μ_{i})^{2} d x

(这个结果的不知道是怎么的得到的，不过不影响分析)
因为第i层是由 $n_{i}$ 个样本的，那么第i层的方差为：

V [F_{i}] = \frac{σ _{i}^{2}}{n _{i}}

总体的方差为：

V [F] = V [i = 1 \sum n v_{i} F_{i}] = i = 1 \sum n V [v_{i} F_{i}] = i = 1 \sum n v_{i}^{2} V [F_{i}] = i = 1 \sum n \frac{v _{i}^{2} σ _{i}^{2}}{n _{i}}

假设每层的样本数量 $n_{i}$ 也是按照权重 $v_{i}$ 分配的，那么 $n_{i} = v_{i} n$ ，则上面的方差可以化简为：

V [F] = \frac{1}{n} i = 1 \sum n v_{i} σ_{i}^{2}

如果不使用分层抽样，而是直接采样，可以把直接采样考虑成随机在所有层中选择了一层，然后随机在这层选择一个样本，那么直接采样的方差为：

V [F] = \frac{1}{n} [i = 1 \sum n v_{i} σ_{i}^{2} + i = 1 \sum n v_{i} (μ_{i} - Q)^{2}]

其中Q是f在 $\land_{i}$ 域上的平均值。从上式可以看出，分层抽样的方差总是小于直接采样的方差，除非每一层的平均值都等于该函数真实的积分值。

重要性采样（Importance Sampling）

重要性采样是蒙特卡洛积分中最有效的提升采样效率的方法，甚至说到蒙特卡洛积分就不得不提到重要性采样。
重要性采样得基本思想是挖掘出最影响估值的(重要)因素，利用好这些因素来估值就能达到减小方差的目的，从而提升采样效率。
以高斯函数 $f (x) = e^{- 1000 (x - 1/2)^{2}}$ 函数为例，它的函数图像为：

如果想要计算它的积分值，就需要在它的定义域 $[0, 1]$ 上采样。这个函数的分布特征非常明显，只有在 $[0.4, 0.6]$ 区间函数值是明显大于0的。假设使用的是均匀采样，在 $[0, 1]$ 内随机选择采样点，那么蒙特卡洛方法得到的结果方差为0.0365。
如果可以找到一个合适的分布，比如以下分布：

p (x) = ⎩ ⎨ ⎧ 0.1 0.91 0.1 x \in [0, 0.45) x \in [0.45, 0.55) x \in [0.55, 1.0)

这个分布的图像为：

这样进行采样的时候，样本主要分布在 $[0.45, 0.55)$ 区间内，与原始的函数大致相符，采样效率就会大大提高，使用这种方法计算出的结果方差大约可以缩小6.7倍。
从上述示例可以看出，计算蒙特卡洛积分时概率密度函数的选择是至关重要的，然而除了独立均匀分布等几种特殊的分布外，许多函数的概率密度函数是难以得到甚至无法获得的，即使可以得到，有的概率密度函数形式非常复杂，没有办法根据它来采样，所以需要找到一个与被积函数形状相似的函数作为pdf，这个过程就是重要性采样。
寻找一个与函数形状相似的pdf是一个比较复杂的过程，在最理想的情况下，希望该pdf为:

p (x) = \frac{f ( x )}{\int f ( x ) d x}

因为这样的话蒙特卡洛估计器：

F_{n} = \frac{1}{n} i = 1 \sum n \frac{f ( X _{i} )}{p ( X _{i} )} = \frac{1}{n} i = 1 \sum n \int f (X_{i}) d x = \int f (x) d x

当然很难的，蒙特卡洛积分就是为了计算 $\int f (x) d x$ 的值，如果事先知道这个值的话就不用计算了。不过从中可以看出，寻找的 $p (x) = c f (x)$ 是一个很好的选择， $p (x)$ 作为新的分布函数，依然要遵循pdf的原则，比如在定义域内的积分为1。

多重重要性采样（MIS）

如果我们需要计算的是多个函数乘积的积分，比如渲染方程：

L_{o} (p, ω_{o}) = L_{e} (p, ω_{o}) + \int_{Ω} f_{r} (p, ω_{i}, ω_{o}) L_{i} (p, ω_{i}) n \cdot ω_{i} d ω_{i}

积分项中包含了 $f_{t}, L_{i}, n \cdot w_{i}$ 三项，使用蒙特卡洛积分进行计算时，如果进行重要性采样，该样本就需要同时考虑这个三个函数的分布。
为了便于讨论，假设要求 $\int f_{a} (d) f_{b} (x) d x$ 的值，并且已经知道了它们的分布 $p_{a} (x)$ 和 $p_{b} (x)$ ，如果采样时只考虑其中一个分布的话，假设只考虑 $p_{a} (x)$ ，则

F_{n} = \frac{1}{n} i = 1 \sum n \frac{f _{a} ( X _{i} ) f _{b} ( X _{i} )}{p _{a} ( X _{i} )}

这个方差是非常大的，同理只考虑 $p_{b} (x)$ 也一样。
多重重要性采样就是为了解决这种多个函数乘积求积分的问题，它的思想是：在对多种分布进行采样时，应该从多个分布中抽取样本，保证样本至少和其中一个分布是相吻合的，然后将每种分布的样本进行加权，以此消除样本与分布不匹配带来的误差。
以上面的函数为例，采用MIS方法，采样时同时考虑两种分布，假设样本 $X \sim p_{a} (x)$ 、 $Y \sim p_{b} (x)$ ，则样本估计器的值为：

w_{a} (X) \frac{f ( X )}{p _{a} ( X )} + w_{b} (Y) \frac{f ( Y )}{p _{b} ( Y )}

其中 $w_{a} (X)$ 和 $w_{b} (Y)$ 是两个分布的权重。
更通用地，MIS可以写成如下形式：

F_{n} = i = 1 \sum n \frac{1}{n _{i}} j = 1 \sum n_{i} w_{i} (X_{i, j}) \frac{f _{i} ( X _{i, j} )}{p _{i} ( X _{i, j} )}

其中 $\sum_{i = 1}^{n} w_{i} = 1$ ，并且当 $p_{i} (x) = 0$ 时 $w_{i} = 0$ 。
于是，寻找合适的权重 $w_{i}$ 就成了MIS中重要的一步。最直观的方法是令 $w_{i} = 1/ n$ ，即每一个分布的权重都是一样的，这个方法固然是可行的，但是稍加思考就可以明白，更好的情况是当样本非常符合函数的分布时，权重应该更大，当样本不太符合函数的分布时，权重应该更小，这样最终的方差才会更小。
实际使用时，一种非常有效的方法是balance heuristic函数，它考虑样本可能产生的所有方式，具体定义为：

w_{i} (x) = \frac{n _{i} p _{i} ( x )}{\sum _{j} n _{j} p _{j} ( x )}

即每个分布函数的权重等于它的采样数量和分布函数的乘积在总的采样数量和分布函数中的权重，假设是一次采样的话，权重就等于该次采样的分布函数占所有分布函数的和的比例。使用这种方式可以有效降低对积分贡献较小的分布所占的比重，也就能减小误差。
balance heuristic函数的实现:

Float BalanceHeuristic(int nf, Float fPdf, int ng, Float gPdf) 
{ 
    return (nf * fPdf) / (nf * fPdf + ng * gPdf); 
}

另一种有效的确定权重的方法叫做power heuristic，它与balance heuristic思想类似，只是分子和分母同时取指数 $β$ ，

w_{i} (x) = \frac{( n _{i} p _{i} ( x ) ) ^{β}}{\sum _{j} ( n _{j} p _{j} ( x ) ) ^{β}}

当 $β = 2$ 时，power heuristic的实现为：

Float PowerHeuristic(int nf, Float fPdf, int ng, Float gPdf) 
{ 
    Float f = nf * fPdf, g = ng * gPdf; 
    return Sqr(f) / (Sqr(f) + Sqr(g)); 
}

MIS唯一的缺陷在于，当样本非常符合被积函数中的其中某一个分布时，方差会增加。

多重重要性采样补偿（MIS Compensation）

TODO
不是很重要，先略过

俄罗斯轮盘

俄罗斯轮盘也是一种提升蒙特卡洛积分的方法，它的思想是跳过那些对计算结果影响很小的采样，假设我们需要计算的积分项形式为：

\frac{f ( X ) v ( X )}{p ( X )}

渲染方程中积分项有3个，所以这种形式是很常见的。如果 $f (X)$ 的计算结果为0或者非常接近于0，那么 $v (X)$ 的计算是完全没有必要的，因为这一次采样的 $v (X)$ 显然对最终结果影响很小，这一次的采样就可以立即结束。当然这样直接结束可能会引入误差，因为 $f (X)$ 接近于0的时候 $v (X)$ 的结果还是会贡献此次采样的值，但俄罗斯轮盘可以消除这些误差。
在俄罗斯轮盘中，首先确定一个终止概率（termination probability）q，这个概率是可以人为确定的，比如在渲染中，随着光线的不断弹射，它每一次弹射”采集到“的光照强度对当前像素计算结果的贡献会越来越小，那么我们就可以让q随着光线弹射的次数增加而增加，这样弹射次数越多，该路径终止的概率越大。当此次采样在概率q之内时，表示此次采样应该终止，使用一个常数c来代替此次采样的结果，为了方便，通常可以使 $c = 0$ ；当此次采样在概率q之外时，此次采样正常计算，但是最终的计算结果要除以 $1 - q$ ，这是为了补偿之前终止的采样。
使用这种方法，新的估计器就可以表示为:

F^{'} = {\frac{F - q c}{1 - q} c ξ > q o t h er w i se

它的数学期望：

E [F^{'}] = (1 - q) \frac{E [ F ] - q c}{1 - q} + q c = E [F]

还是与原来的数学期望是一样的。
使用俄罗斯轮盘并不会降低蒙特卡洛积分的误差，反而会引入一些误差，但是它可以非常有效地提升采样效率，在光线追踪渲染时基本都会使用这种方法。

分割

当对二维积分进行计算时，比如：

\int_{A} \int_{B} f (x, y) d x d y

按照通常的蒙特卡洛积分方法，应该在定义域A和B上共取n个随机变量，假设 $X \sim p_{x}$ 、 $Y \sim p_{y}$ ，则蒙特卡洛估计器的值为：

\frac{1}{n} i = 1 \sum n \frac{f ( X _{i} , Y _{i} )}{p _{x} ( X _{i} ) p _{y} ( Y _{i} )}

使用分割的方法可以在采样时先确定A上的一个样本X，再在X的基础上在定义域B上确定一个样本Y，于是蒙特卡洛估计器的值就为：

\frac{1}{n} i = 1 \sum n \frac{1}{m} j = 1 \sum m \frac{f ( X _{i} , Y _{i, j} )}{p _{x} ( X _{i} ) p _{y} ( Y _{i, j} )}

假设可以先计算 $f (X_{i}, y)$ ，这种方法相当于采样 $nm$ 个样本，它的效率会比第一种方法更高。

使用逆变换采样法（Inversion Method）采样

直到现在为止，蒙特卡洛积分中还有一个重要的步骤是未知的，那就是如何通过选择的概率分布来生成随机样本。如果只是简单的独立均匀分布，当然可以通过在定义域 $[a, b]$ 区间内随机生成数字来作为样本，因为此时概率密度函数是一个常数，但大多数情况下概率分布都没有这么简单。通过概率分布来生成随机数的技术有多种，在渲染中最常用的叫做逆变换采样法，它通过求CDF的反函数，将 $[0, 1)$ 上均匀的样本映射到给定的概率分布上。

离散型随机变量

假设有一个离散型随机变量，它有4种可能，其概率分别为 $p_{1}, p_{2}, p_{3}$ 和 $p_{4}$ ，所有的概率相加为1，且它的PMF如下所示：

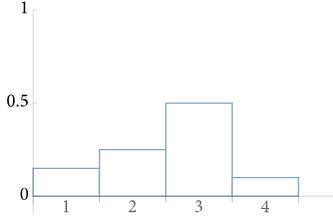
从上图可以看出， $p_{3}$ 最大， $p_{4}$ 最小。
计算该变量的CDF，结果如下图所示：

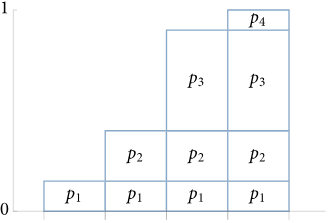
此时在纵坐标轴上取一个随机值 $ξ$ ，很明显 $ξ \in [0, 1]$ ，如下图所示：

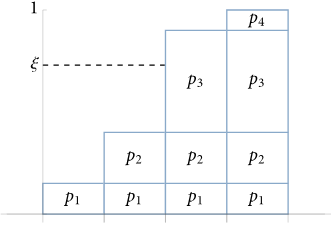
那么 $ξ$ 对应的横坐标区域就是它的PMF。
这就是逆变换采样法的名称由来，通常情况下，都是使用横坐标即随机变量的值来求它的CDF，这里反其道而行之，在CDF上取值来映射到随机变量的值，并得到它的PMF。在上面的示例图中， $ξ$
对应的随机变量的值为 $X \sim p_{3}$ ，所以此次样本的PMF即为 $p_{3}$ 。
通过观察上图也可以看出，在取随机值 $ξ$ 时，取到 $p_{3}$ 区间的概率是最大的，而取到 $p_{4}$ 区间的概率是最小的，与原随机变量的概率分布相符。

使用这种方法采样的操作实际上就是通过生成一个随机数 $ξ \in [0, 1)$ ，根据这个随机数找到该随机变量的某一个样本值和该样本对应的概率（PMF），这样该样本就可以用来做蒙特卡洛积分的计算了。
下面是一个离散随机变量采样的实现函数，它接收该变量的各个取值的权重（该权重并不一定标准化，即它们的和不一定等于1）weights，一个随机生成的 $[0, 1)$ 区间的数u，返回该次采样的值（这里是返回weights的偏移，由于每一个weight都会对应一个随机值，所以通过这个weights的偏移很容易获得具体的值），得到该次采样的pmf和u重新映射的值。
代码来自PBRT书籍：

int SampleDiscrete(pstd::span<const Float> weights, Float u, Float *pmf, Float *uRemapped) { 
    // 处理特殊情况
    if (weights.empty()) { 
        if (pmf) 
            *pmf = 0; 
        return -1; 
    }
    // 由于weights不是标准化的，所以sumWeights不一定是1
    Float sumWeights = 0; 
    for (Float w : weights) 
        sumWeights += w;
    // u是从[0,1)中取得，这里映射到[0, sumWeights)，这里考虑了浮点数的精度问题
    Float up = u * sumWeights; 
    if (up == sumWeights) 
        up = NextFloatDown(up);
    // 求up对应的offset，满足CDF(offset-1) <= up < CDF(offset)
    int offset = 0; Float sum = 0; 
    while (sum + weights[offset] <= up) 
        sum += weights[offset++];
    // 计算对应的pmf，并将up映射回[0,1)
    if (pmf) 
        *pmf = weights[offset] / sumWeights; 
    if (uRemapped) 
        *uRemapped = std::min((up - sum) / weights[offset], OneMinusEpsilon);
 
    return offset; 
}

其中uRemapped并不是一个必选项，它将u经过映射后又映射回 $[0, 1)$ ，这在某些随机数生成算法中可能会有用处。

连续型随机变量

在连续型随机变量中，逆变换采样法的思想是一样的，但是具体的做法需要改进。
假设已经知道的随机变量的PDF为 $p (x)$ ，通过以下步骤来进行采样：

使用PDF来计算CDF，计算方法为 $P (x) = \int_{- \infty}^{x} p (t) d t$ 。（这里假设该随机变量的定义域从负无穷开始）
生成一个规范的随机数 $ξ$ 。
通过 $P (X) = ξ$ 来计算样本X的值。这里也可以先计算CDF的反函数 $P^{-} 1 (x)$ ，再计算 $X = P^{-} 1 (ξ)$ 。

连续型随机变量采样示例—对线性插值函数进行采样

线性插值函数是渲染中常用的函数之一，它的形式是

f (x) = (1 - x) a + x b

其中 $x \in [0, 1]$ ，这个函数根据变量x在a和b之间进行插值。假设现在需要使用蒙特卡洛积分求它的某个组合函数在一个定义域上的积分值（这个函数本身求积分是可以直接计算出来的），那么需要根据这个函数的分布对它进行采样，根据上面对连续型随机变量的采样步骤，具体的做法如下：

第一步：确定这个线性插值函数的pdf，然后求出它的cdf。
非常幸运的是这个函数在其定义域上的积分是可以计算的， $\int_{0}^{1} f (x) d x = \frac{a + b}{2}$ ，根据重要性采样（Importance Sampling）章节介绍的求pdf的方法，可以求得它的pdf为：

p (x) = \frac{2 f ( x )}{a + b}

用代码来实现（代码来自PBRT）：

float LineraPDF(float x, float a, float b)
{
    if(x < 0 || x > 1)
        return 0;
    return 2 * Lerp(x, a, b) / (a + b);
}

知道了pdf之后，求出这个函数的cdf，

P (x) = \int_{0}^{x} p (x) d x = \frac{x ( a ( 2 - x ) + b x )}{a + b}

第二步：生成随机变量 $ξ$ ，通过函数的cdf计算对应的采样值 $X$ 。
生成一个 $[0, 1]$ 间的随机值 $ξ$ 后，通过 $P (X) = ξ$ 就可以得到此次采样的值 $X$ ，可以求得

X = \frac{a - ( 1 - ξ ) a ^{2} + ξ b ^{2}}{a - b}

为了防止 $a = b$ 时除数为0，一般将其化为如下形式（平方差公式）

X = \frac{ξ ( a + b )}{a + ( 1 - ξ ) a ^{2} + ξ b ^{2}}

代码实现：

Float SampleLinear(Float u, Float a, Float b) 
{ 
    if (u == 0 && a == 0) 
        return 0;
    Float x = u * (a + b) / (a + std::sqrt(Lerp(u, Sqr(a), Sqr(b))));
    return std::min(x, OneMinusEpsilon); 
}

分布的变换

上面逆变换采样法只介绍了针对一维随机变量的采样方法，然而在渲染中，多维随机变量的采样非常常见，在一张图片上随机采样时，需要生成二维随机变量的样本，在空间中对某个方向进行采样时，需要生成三维随机变量的样本。
接下来研究如何使用同样的方法来采样多维的随机变量。

一维随机变量的分布变换

假设有一个随机变量x，它的cdf为 $P (x)$ ，pdf为 $p (x)$ ，另一个随机变量 $y = f (x)$ ，如果 $f (x)$ 是连续且单调的，那么根据cdf的定义，

P (x) P_{y} (y) = p (X \leq x) = p_{y} (Y \leq f (x)) = p (X \leq f^{- 1} (y)) = P (f^{- 1} (y))

根据pdf和cdf的关系，可求得

p_{y} (y) = ∣ \frac{df}{d x} ∣^{- 1} p (x)

更加直观的写法：

p_{y} (y) = p (h (y)) ∣ h^{'} (y) ∣

其中h(y)是f(x)的反函数。这就是概率密度变换公式。
这里加了绝对值符号是为了让 $f (x)$ 单调递增和递减的情况都能适用。
举一个例子，x的pdf为 $p (x) = 2 x, x \in [0, 1]$ ，现在 $y = f (x) = s in (x)$ ，很明显f(x)在区间 $[0, 1]$ 内是单调递增的，现在要求y的pdf，求解的过程为：

h (y) p_{y} (y) = a rcs in (y) = p (h (y)) ∣ h^{'} (y) ∣ = p (a rcs in (y)) ∣ \frac{1}{1 - y ^{2}} ∣ = \frac{2 a rcs in ( y )}{1 - y ^{2}}

有了 $p_{y} (y)$ ，就可以使用逆变换采样法进行采样了。

多维随机变量的分布变换

与一维随机变量相似，多维随机变量之间的变换也是有变换公式的。
在多维随机变量中，概率的分布使用联合概率密度函数表示，对应了一维随机变量中的概率密度函数。这里以二维随机变量为例，更多维的随机变量也是类似的。
假设存在二维随机变量x, y，它们的联合概率密度为 $f_{x, y} (x, y)$ ，现有随机变量 $u = g (x, y), v = h (x, y)$ ，则称u,v为x,y的变换，u,v的联合概率密度求解方法如下。
如果函数 $g, h$ 存在连续的偏导数且存在唯一的逆变换，假设它们的逆变换为：

{x = g^{- 1} (u, v) y = h^{- 1} (u, v)

则(u,v)的联合概率密度为

f_{u, v} (u, v) = f_{x, y} (g^{- 1} (u, v), h^{- 1} (u, v)) ∣ J ∣

其中J为变换函数的雅可比行列式，

J = \frac{\partial g ^{- 1}}{\partial u} \frac{\partial h ^{- 1}}{\partial u} \frac{\partial g ^{- 1}}{\partial v} \frac{\partial h ^{- 1}}{\partial v}

以笛卡尔坐标系变换到极坐标系为例，假设现在坐标中随机变量(x, y)的联合概率密度为 $p_{x, y} (x, y)$ ，根据坐标系的转换关系：

r θ = (x^{2} + y^{2}) = a rc t an (\frac{y}{x})

求 $(r, θ)$ 的联合概率密度。
首先，根据上面的转换关系，可以求得它们的逆变换：

x = rcos θ y = rs in θ

然后求雅可比行列式

J = cos θ s in θ - rs in θ rcos θ = r (co s^{2} θ + s i n^{2} θ) = r

所以 $(r, θ)$ 的联合概率密度为

p (r, θ) = r p_{x, y} (rcos θ, rs in θ)

同样的方法也可以用在三维坐标场景，类似地，在三维笛卡尔坐标系和极坐标系下，联合概率密度的转换关系为：

p (r, θ, φ) = r^{2} s in θ p_{x, y, z} (rs in θ cos φ, rs in θ s in φ, rcos θ)

多维随机变量的采样

在知道了多维随机变量之后，同样使用逆变换采样对其进行采样，假设随机变量(x,y)的联合概率密度为p(x,y)，如果x和y是相互独立的，一般来说p(x,y)是通过它们各自的概率密度求得的，即

p (x, y) = p_{x} (x) p_{y} (y)

这时按照它们各自的概率密度采样就可以了。
在大多数情况下，x和y都不是独立的，此时对它们的采样就需要使用另一种方法，首先，先求出x的边缘概率密度,

p (x) = \int p (x, y) d y

这个概率密度就可以作为随机变量x的概率密度，它表示了在所有y可能的取值下x的分布。
然后求y的条件概率密度，计算方法为

p (y ∣ x) = \frac{p ( x , y )}{p ( x )}

这个条件概率密度就是随机变量y的分布。
在更高维的随机变量下，采样的方法也是一样的，先求其中一个随机变量的边缘概率密度，再求其他随机变量的条件概率密度，每一次操作都会让变量的维数减一，直到剩余一维随机变量为止。

多维随机变量采样示例—对双线性插值函数进行采样

双线性插值函数的形式为：

f (x, y) = (1 - x) (1 - y) w_{0} + x (1 - y) w_{1} + y (1 - x) w_{2} + x y w_{3}

其中 $w_{i}$ 为插值的权重，同样使用之前求pdf的方法，可以求得

p (x, y) = \frac{4 f ( x , y )}{w _{0} + w _{1} + w _{2} + w _{3}}

代码实现（PBRT）：

Float BilinearPDF(Point2f p, pstd::span<const Float> w) 
{ 
    if (p.x < 0 || p.x > 1 || p.y < 0 || p.y > 1) 
        return 0; 
    if (w[0] + w[1] + w[2] + w[3] == 0) 
        return 1; 
    return 4 * ((1 - p[0]) * (1 - p[1]) * w[0] + p[0] * (1 - p[1]) * w[1] + (1 - p[0]) * p[1] * w[2] + p[0] * p[1] * w[3]) / (w[0] + w[1] + w[2] + w[3]);
}

这是一个二维的随机变量，首先要从联合概率密度中求得边缘概率密度，这里选择求y的边缘概率密度：

p (y) = \int_{0}^{1} p (x, y) d x = 2 \frac{( 1 - y ) ( w _{0} + w _{1} ) + y ( w _{2} + w _{3} )}{w _{0} + w _{1} + w _{2} + w _{3}}

可以发现，将常数 $\frac{2}{w _{0} + w _{1} + w _{2} + w _{3}}$ 先忽略, $p (y)$ 是一个线性插值的函数。
用之前的线性插值函数来采样，

p.y = SampleLinear(point.y, w[0] + w[1], w[2] + w[3]);

再来求x的条件概率密度：

p (x ∣ y) = \frac{p ( x , y )}{p ( y )} = \frac{2 f ( x , y )}{( 1 - y ) ( w _{0} + w _{1} ) + y ( w _{2} + w _{3} )}

现在y对于 $p (x ∣ y)$ 来说也是常数，现将其忽略，可以发现 $p (x ∣ y)$ 只与 $f (x, y)$ 相关，将 $f (x, y)$ 看作以下形式：

f (x, y) = (1 - x) [(1 - y) w_{0} + y w_{2}] + x [(1 - y) w_{1} + y w_{2}]

则 $p (x ∣ y)$ 也可以看作一个线性插值函数。

p.x = SampleLinear(point.x, lerp(p.y, w[0], w[2]), lerp(p.y, w[1], w[3]));

这样采样点p的坐标就确定了。
双线性插值函数(PBRT)：

Point2f SampleBilinear(Point2f u, std::span<const Float> w)
{
    Point2f p;
    p.y = SampleLinear(u.y, w[0] + w[1], w[2] + w[3]);
    p.x = SampleLinear(u.x, lerp(p.y, w[0], w[2]), lerp(p.y, w[1], w[3]));
    return p;
}

🪴 Quartz 4.0

Explorer

蒙特卡洛积分和采样

背景