路径追踪

在路径追踪中，简单介绍了路径追踪的算法原理和实现方案，而在实际的渲染器中，基于递归的路径追踪算法通常是不会被采用的。路径追踪算法通常需要运行在GPU上，而GPU上不允许出现递归函数，这是GPU的硬件架构决定的，即使算法运行在CPU上，递归带来的性能损失依然无法接受。
这里对路径追踪算法进行更深入的研究，重点探索它的算法实现方案。资料来源于PBRT书籍。

光线传输方程（Light Transport Equation）

光线传输方程（LTE）用于描述场景中辐射率的分布，它通过物体表面自发光属性、BSDF以及到达该点的入射辐射率，计算出某一个点的反射辐射率。

基础理论

首先，LTE的基础是能量守恒定律。光线传输过程中，系统的输出能量与输入能量之差，等于系统的辐射能量与吸收能量之差。对于一个物体来说，离开它的能量${\Phi }_o$，进入它的能量${\Phi }_i$，它发射的能量${\Phi }_e$和它吸收的能量${\Phi }_a$之间满足以下关系。

$${\Phi }_o-{\Phi }_i={\Phi }_e-{\Phi }_a$$

在这个前提下，假设光线在传输过程中没有能量损耗，如下图所示，如果要计算p点在$\omega$上的入射辐射率，只需计算沿$\omega$方向上光线与场景的交点p’在$-\omega$方向的出射辐射率即可，如下图所示：

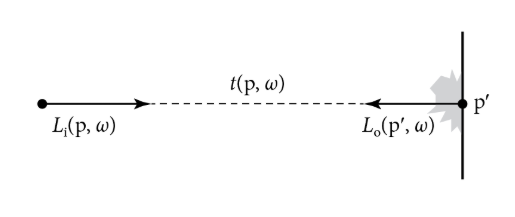
可以用公式来表示：

$$L_i(p,\omega )=L_o(t(p,\omega ),-\omega )$$

其中t表示光线投射函数（ray-casting function），用来计算光线(p, $\omega$)在场景中的交点p’。
这样就可以把渲染方程写成如下形式：

$$L(p,{\omega }_o)=L_e(p,{\omega }_o)+{\int }_{\Omega }{f}_r(p,{\omega }_i,{\omega }_o)L(t(p,\omega ),-{\omega }_i)n\cdot {\omega }_{i}d{\omega }_i$$

这就是LTE方程。
通过规定场景中的能量守恒，就把这个方程左右两边的L统一了。

面积的LTE方程

LTE方程中目前还是带有太多的变量，为了方便，需要将对立体角的积分转换位对面积的积分。
首先，将辐射率的表示方法进行如下转换：

$$L(p^{\prime }\to p)=L(p^{\prime },\omega )$$

这表示从p’点传播到p点的辐射率。
同时，修改BRDF函数的表示方式：

$$f(p^{\prime \prime }\to p^{\prime }\to p)=f(p^{\prime },{\omega }_o,{\omega }_i)$$

这表示p’点的BRDF值，很明显这里${\omega }_i=p^{\prime \prime }-p^{\prime }$，${\omega }_o=p-p^{\prime }$。

将立体角微分转换为面积微分

这是研究LTE方程的重要数学工具，在上面的LTE方程中，是对立体角$\omega$进行积分，这里需要将其转换为对面积A的积分。
在立体角（solid angle）中介绍过，立体角的定义是

$$\Omega =\frac{A}{r^2}$$

这是一个线性关系的函数，所以有

$$d\omega =\frac{dA}{r^2}$$

这里的面积A指的是立体角所在圆上的面积，而我们要计算场景中任意一点的面积，它并不位于圆上（其法线与立体角方向并不相同），如果用A’表示场景中任意一点p’处的面积，根据Lambert的余弦定理，有

$$dA=d{A}^{\prime }\cos {\theta }^{\prime }$$

其中${\theta }^{\prime }$表示p’处的法线与立体角$\omega$的夹角。

Note

这里的$\cos {\theta }^{\prime }$严格来说应该是$|\cos {\theta }^{\prime }|$，要取绝对值，这里为了方便做了不严谨的简化，但是程序中肯定是不能计算出负数的面积或辐射率的

这样，立体角微分和面积微分的关系就可以表示出来了，

$$d\omega =\frac{\cos \theta }{r^2}dA$$

回到LTE方程，更近一步使用函数G来表示可见性加方程中的$\cos \theta$项，以及立体角微分转换面积微分的项，

$$G(p\leftrightarrow p^{\prime })=V(p\leftrightarrow p^{\prime })\frac{\cos \theta \cos {\theta }^{\prime }}{||p-p^{\prime }|{|}^2}$$

其中V表示p点和p’点的可见性，为0时表示二者不可见，为1时表示二者可见。
$\cos \theta$表示p点法线与(p-p’)方向的余弦积（绝对值）。
$\cos \theta$’表示p‘点法线与(p-p’)方向的余弦积（绝对值）。
$||p-p^{\prime }|{|}^2$表示p点和p’点距离的平方。
通过这些表示，就可以使用面积的积分来表示LTE方程了，

$$L(p^{\prime }\to p)=L_c(p^{\prime }\to p)+{\int }_{A}f(p^{\prime \prime }\to p^{\prime }\to p)L(p^{\prime \prime }\to p^{\prime })G(p^{\prime \prime }\leftrightarrow p^{\prime })dA(p^{\prime \prime })$$

p点表示观察点，也就是相机位置。
p’点是直接观察到的场景中的点。
p”点是对p’点有间接光照共享的点。

路径积分