渲染一张2D图片,实际上就是使用离散的像素点去描述真实世界的场景。在光线追踪算法中,需要通过光线去“采样”场景中的信息,然后”重建“在计算机的屏幕上。一般来说,“采样”指的是使用一些样本去获得某个连续函数的特征,而重建指的是通过采样获得的特征去还原原来的连续函数。
下面是一个采样一维函数并重建的示意图(PBRT):
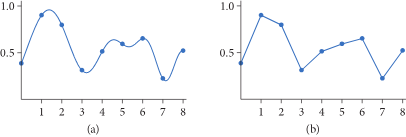
在图(a)中采样了9个样本并计算了它对应的样本值,然后在图(b)中使用这些样本值来尝试重建原来的函数,这个重建并不精确,因为样本信息不够完善。
采样与重建更深入的理论需要了解傅里叶变换(Fourier Transform),简单来说傅里叶变换可以把一个函数变换为多个三角函数来表示,这样就可以得到函数的频率信息,然后根据时域的卷积等于频域的乘积:( ,就可以根据频域去制定样本。
这里暂时不做深入的研究,简单了解一下傅里叶变换的公式:
它的逆变换为:
一般来说,采样就是将脉冲函数与被采样函数相乘,脉冲函数的定义为:
对函数进行采样,可以表示为:
使用图像表示为:

(a)为被采样函数,(b)为脉冲函数,(c)为采样结果。
而重建的过程可以表示为将采样结果与滤波函数求卷积,卷积的定义为:
其中被称为约束变量。卷积运算的定义有点复杂,这里暂时记住有这么一个运算就行。
对函数重建的过程可以表示为:
其中滤波函数有多种,常用的有盒型滤波和高斯滤波等。
在对二维图像的处理中,卷积其实就是将一个卷积核与图像对应位置的像素进行相乘并相加,得到对应输出位置上的像素。
采样与积分
在渲染中,通常使用蒙特卡洛积分来进行渲染方程的求解,在求解的过程中,一个好的采样分布直接影响到积分的收敛速度,所以在设计渲染算法时,一个可以生成优秀分布的样本点的采样算法是非常重要的。
Discrepancy
什么是一个优秀的样本分布,通常使用Discrepancy来衡量,它的定义是:
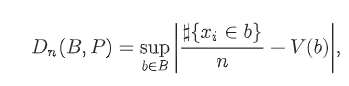
这个公式不需要做太深入的理解,简单来说就是在单位区域P点集中随机选择一个区域B,B中的采样点数量与总采样点数量的比值与B的体积相差得越小,那么这些样本的Discrepancy就越小,这些样本的分布就越优秀。通俗的理解就是优秀的样本分布应该是样本均匀地分布在整个样本空间。如果一个序列的Discrepancy很小,那么就称它是一个低差序列(Low Discrepancy Sequence)。
在程序中,采样时一般都是从一个伪随机数序列中选取样本,所以,一个好的采样算法应该是可以生成低差序列的。
采样器的设计(PBRT)
采样器(Sampler)用来生成样本点,在渲染中可以使用这些样本进行蒙特卡洛积分的计算,不同的生成算法将会影响到渲染的最终效果和渲染效率。
采样器需要根据不同的情况生成不同维度的采样点,因为在渲染方程中,不同阶段的光线可能需要不同维度的样本。
采样器的基类
定义一个采样器的基类:
class Smapler
{
...
};首先,它需要提供每个像素的采样数,这个变量可以作为成员变量保存起来,一般在渲染系统初始化的时候确定。
int SamplesPerPixel() const;然后,采样器需要有一个StartPixelSample方法,在最开始生成camera ray时由Integrator调用,Integrator需要提供采样像素的坐标和采样的索引,采样的索引标识当前像素正在进行第几个样本的采样,它应该大于0但是小于等于每个像素的采样数(SamplesPerPixel的返回值),Integrator也可以指定从第几个样本进行采样,
void StartPixelSample(Point2i p, int sampleIndex, int dimension = 0);这样做的目的有两个,第一,让采样器知道此次采样的索引,可以利用算法对样本进行优化,防止临近的两次采样取得相近的样本值;第二,可以在最开始进行初始化时就确定采样器的状态,采样器将为固定的采样索引提供相同的样本值,这样方便程序的debug并且不影响渲染结果。
接下来,采样器需要提供两个接口来返回采样获得的一维和二维样本,更高维的样本在渲染算法中一般不需要,需要时也可以将这两个低维的样本组合,
Float Get1D();
Point2f Get2D();最后是一个可选的接口GetPixel2D,它专门用来生成flim某个像素中的坐标点,有的子类会实现它,有的子类只在其中调用Get2D方法,
Point2f GetPixel2D();Independent Sampler
这是一个最简单的采样器,它生成一些独立均匀的样本,不考虑任何优化采样的措施,在渲染时一般只用于测试。
class IndependentSampler public Smapler
{
...
};IndependentSampler中有一个伪随机的随机数生成器,设置不同的seed它就会生成不同的随机数,
class IndependentSampler public Smapler
{
public:
IndependentSampler(int samplesPerPixel, int seed = 0) : samplesPerPixel(samplesPerPixel), seed(seed) {} // 构造函数
...
private:
int samplesPerPixel, seed;
RNG rng; // 随机数生成器
};其中RNG的状态要在每次使用完毕后重置,这样就可以保证每一次生成都是独立的。
接下来实现StartPixelSample方法,制定一个像素点的坐标和该像素的采样索引,“激活”这个采样器,
void StartPixelSample(Point2i p, int sampleIndex, int dimension) {
rng.SetSequence(Hash(p, seed));
rng.Advance(sampleIndex * 65536ull + dimension);
}RNG使用SetSequence生成一个随机数序列,使用Advance指定这个序列的偏移,这样就可以保证同一个像素点的同一个采样索引生成的样本值是相同的,同时sampleIndex可以保证不同的样本值在序列中不会位于相近的地方。
接下来获取样本值的方法就比较简单了,直接使用rng生成随机数即可,
Float Get1D() { return rng.Uniform<Float>(); }
Point2f Get2D() { return {rng.Uniform<Float>(), rng.Uniform<Float>()}; }
Point2f GetPixel2D() { return Get2D(); }这个采样器采样的效果非常不好,独立均匀的样本往往会在图片中产生很多噪点,但它已经是一个可以正常工作的采样器了,它的实现也非常清晰可观。
Halton Sampler
Halton采样器可以通过生成低差序列来得到一个更好的样本分布,它的采样效率会比Independent更高。
Radical Inversion
这是构造Halton采样器的基础思想,它的定义为:
它的含义是,对于一个正整数b,将任何一个整数i表示为b进制的数,然后把每一位上的数字组成一个向量,和一个矩阵C相乘得到一个新的向量,再把这个新向量中的数字镜像到小数点右边。这样得到的小数称为以b为底数,以C为生成矩阵的radical Inversion。
Van der Corput序列
为了方便,先假设C是一个单位矩阵,这样乘以矩阵的过程就可以先忽略,整个过程就变成了把b进制的各个位上的数镜像到小数点右边。这就是Van der Corput序列。
举个例子,假设i = 8,b = 2,将8以二进制表示,得到1000,然后镜像小数点到右边,得到0.0001,转换为10进制就是0.0625,所以。下表为以而为底的Van der Corput序列例子。
| i | Base2 | |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 0.1 = 1/2 |
| 2 | 10 | 0.01 = 1/4 |
| 3 | 11 | 0.11 = 3/4 |
| 4 | 100 | 0.001 = 1/ 8 |
| … | … | … |
| Van der Corput有以下属性: |
- 每一个新的样本点都会落在当前样本点“最稀疏的区域”。
- 样本点个数达到个时会对形成均匀的划分,比如上面样本点个数为4时,刚好4等分单位区间。
- 很多时候并不能够替代伪随机数,因为样本值与索引有很大关系。
Halton序列和Hammersley点集
Halton序列定义如下:
确定样本点索引i,n维的Halton序列的每一个维度都是基于不同的底数的Van der Corput序列,通常来说,所使用的底数互质,比如。
Hammersley点集定义如下:
与Halton序列唯一不同的是将第一位的序列改成了,N为样本的个数。
下图为Halton序列和Hammersley点集分别生成216个2维样本点的图(选择的radical Inversion低为2和3):
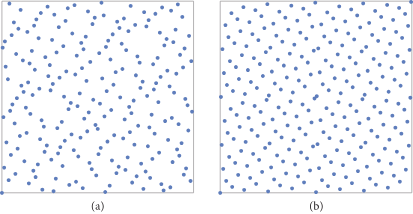
图(a)为Halton序列,
图(b)为Hammersley点集,
从上图中可以看出Hammersley点集比Halton序列的样本分布得更加均匀,但是Hammersley点集生成必须预先知道N的大小(即总样本个数),而Halton序列没有这个限制。
Radical Inversion算法的实现(PBRT)
Float RadicalInverse(int baseIndex, uint64_t a)
{
// base通过索引从质数列表中取
int base = Primes[baseIndex];
Float invBase = (Float)1 / (Float)base, invBaseM = 1;
uint64_t reversedDigits = 0;
while (a) {
// 将a看作base进制的数的话,digit是最后一位的数字,next是去掉最后一位剩下的数字
// 即digit = a % base;
uint64_t next = a / base;
uint64_t digit = a - next * base;
// 将数字累加到reversedDigits
reversedDigits = reversedDigits * base + digit;
// 每取一位,invBaseM就会缩小Base倍,用来将数字镜像到小数点后边
// 每乘以一次invBase,最终结果的小数点就会向左移动一位
invBaseM *= invBase;
a = next;
}
// 保证结果不会大于1
return std::min(reversedDigits * invBaseM, OneMinusEpsilon);
}Randomization via Scrambling(通过扰乱进行随机化)(这一节没有完全理解)
Halton序列和Hammersley点集固然是非常优秀的低差序列,但是它们有一个缺点,当使用的底数b增大时,样本的分布并不是特别均匀,事实上,只有点的数量接近于b的幂时样本分布才是最均匀的。(上面以2和3为底数时生成了216个样本,因为。)
如果底数b太大,而生成的样本点数不多,那么它们随机均匀分布的性质就会大打折扣。为了解决这个问题,需要使用扰乱(Scrambling)的方法来保证样本的随机性。扰乱的方法有许多中,对于Halton序列和Hammersley点集来说,一般是在将每一位数字镜像到小数点右边时,通过一组排列(permutations)先将其转换为另一个数字,这种转换并不会影响到样本的随机性,因为Halton序列是将一个域进行均匀的划分,而这种扰乱只是影响划分的顺序。
permutations的生成方法也很多,构造好的permutations也可以减少积分的错误,为了简单起见,先只考虑随机生成的permutations。
下面是PBRT中的算法实现:
对于一个底数base,DigitPermutation类用于生成和保存它的permutations,
class DigitPermutation
{
public:
DigitPermutation(int base, uint32_t seed, Allocator alloc)
: base(base)
{
// 先计算出此base的Permutation长度
// Permutation长度的长度需要达到(base - 1) * invBaseM接近于0为止
// 以base=3为例,它的Permutation长度要达到2 * invBaseM接近于0,也就是在3进制中,将整数2的小数点一直左移,直到它接近于0
// 这个nDigits表示当RadicalInverse的数经过RadicalInverse运算后出现了这么多位时,就可以从此截断了
nDigits = 0;
Float invBase = (Float)1 / (Float)base, invBaseM = 1;
while (1 - (base - 1) * invBaseM < 1) {
++nDigits;
invBaseM *= invBase;
}
// 分配内存空间
permutations = alloc.allocate_object<uint16_t>(nDigits * base);
// 计算permutations
for (int digitIndex = 0; digitIndex < nDigits; ++digitIndex) {
// 生成随机的哈希值
uint64_t dseed = Hash(base, digitIndex, seed);
// 每base个数一组,生成nDigits组
for (int digitValue = 0; digitValue < base; ++digitValue) {
int index = digitIndex * base + digitValue;
// PermutationElement基于base生成随机排列,比如base = 3,这一次循环可能生成 (2, 1, 0)
permutations[index] = PermutationElement(digitValue, base, dseed);
}
}
}
private:
int base, nDigits;
uint16_t *permutations;
};DigitPermutation类提供一个Permute方法根据index和value返回排序数值,
int Permute(int digitIndex, int digitValue) const {
return permutations[digitIndex * base + digitValue];
}有了这个工具类之后,可以针对每一个素数生成一个DigitPermutation,具体的代码省略。
最后,加了随机扰乱的RadicalInverse实现:
Float ScrambledRadicalInverse(int baseIndex, uint64_t a,
const DigitPermutation &perm) {
int base = Primes[baseIndex];
Float invBase = (Float)1 / (Float)base, invBaseM = 1;
uint64_t reversedDigits = 0;
int digitIndex = 0;
while (1 - (base - 1) * invBaseM < 1) {
uint64_t next = a / base;
int digitValue = a - next * base;
// digitValue通过perm.Permute进行扰乱
reversedDigits =
reversedDigits * base + perm.Permute(digitIndex, digitValue);
invBaseM *= invBase;
++digitIndex;
a = next;
}
return std::min(invBaseM * reversedDigits, OneMinusEpsilon);
}Halton Sampler实现
有了上面的理论和工具,现在可以实现Halton Sampler了。
Halton Sampler的实现与Independent Sampler有一些差异,Independent Sampler可以单独地为每一个像素生成采样点,Stratified Sampler(分层采样器)也一样,只要设置好像素的索引,每一次生成的样本点都是固定的。而Halton Sampler是一次为所有像素生成样本值,具体来说,对于2维的图片,Halton Sampler生成分布在的样本,然后再将其扩展到width * height的二维空间中,这样也可以保证同一个像素的同一个索引获得的样本值是一样的。所以Halton Sampler需要预先提供分辨率fullRes。
Halton Sampler的定义:
class HaltonSampler
{
public:
HaltonSampler::HaltonSampler(int samplesPerPixel, Point2i fullRes,
RandomizeStrategy randomize, int seed, Allocator alloc)
: samplesPerPixel(samplesPerPixel), randomize(randomize) {
// 计算digitPermutations
if (randomize == RandomizeStrategy::PermuteDigits)
digitPermutations = ComputeRadicalInversePermutations(seed, alloc);
/*
这里选择的base为2和3,并且计算出覆盖到整个分辨率的缩放比例,即2^j和3^k,这里限制最大分辨率不能超过128*128,这是为了保证浮点数的精度,当真实分辨率超过这个值时,可以重复“铺贴”来覆盖整个图片。
*/
for (int i = 0; i < 2; ++i) {
int base = (i == 0) ? 2 : 3;
int scale = 1, exp = 0;
while (scale < std::min(fullRes[i], MaxHaltonResolution)) {
scale *= base;
++exp;
}
baseScales[i] = scale;
baseExponents[i] = exp;
}
// 计算乘法逆元x (m * x) mod n = 1
multInverse[0] = multiplicativeInverse(baseScales[1], baseScales[0]);
multInverse[1] = multiplicativeInverse(baseScales[0], baseScales[1]);
}
private:
int samplesPerPixel;
RandomizeStrategy randomize; // 定义了扰乱的类型
pstd::vector<DigitPermutation> *digitPermutations = nullptr; // 保存了所有素数的Permutation
static constexpr int MaxHaltonResolution = 128;
Point2i baseScales, baseExponents;
int multInverse[2];
int64_t haltonIndex = 0;
int dimension = 0;
}RandomizeStrategy定义的几种扰乱类型:
enum class RandomizeStrategy { None, PermuteDigits, FastOwen, Owen };通过上面的计算,可以知道,假设构建的分辨率为,每个像素采样n个顶点,那么一共会生成个采样点,这时进行采样时,就需要将采样点与sampleIndex和样本点的全局索引haltonIndex关联起来。
Sobol Samplers
…
Filter的设计
从采样与重建的理论中可以知道,一个完整的渲染过程,在将场景通过采样器进行采样之后,还需要将采样结果与滤波器(filter)卷积才可以得到最终的图像。
想要使用filter重建出完美的原始函数是不可能的,所以,在渲染中所有的filter都只能尽量还原场景,并不存在一种最优的filter,根据不同的场景选择不同的filter才能达到最好的渲染效果。
Filter Interface
所有的filter都是一个“波峰“状的函数,通常中心位于原点然后在一个范围内变化为0,这个变为0的距离被称为它的radius,如下图所示(实际的使用的filter是二维的,因为需要处理的图片是二维的,这里展示它的一个”切面“):

一个filter在x和y方向上的radius会不一样,接口Radius()返回这个两个方向的radius,
Vector2f Radius() const;接口Evaluate根据一个二维点返回它的函数值,在函数之外的点将返回0,
Float Evaluate(Point2f p) const;接口Integral返回整个filter的积分值,它可以用来对filter进行normalize。
Float Integral() const;FilterSample保存fliter的采样位置和权重,权重表示此位置的函数值与此次采样的pdf的比值,(其实应该返回函数值和它对应的pdf,但是在进行蒙特卡洛积分计算时需要计算它们的比值,这里就先将其计算出来了)
struct FilterSample {
Point2f p;
Float weight;
};接口Sample用于重要性采样,他接受一个区间的二维数据,返回一个FilterSample结构体。
FilterSample Sample(Point2f u) const;FilterSampler
并不是所有的filter都可以轻易地从它们的分布中进行采样,FilterSampler类包装了从一个filter中进行采样的方法。
FilterSampler部分定义如下:
class FilterSampler {
public:
...
private:
Bounds2f domain; // filter的x, y边界
Array2D<Float> f; // 二维数组,保存了filter在(x, y)处的值
PiecewiseConstant2D distrib; // filter分布
};构造函数:
FilterSampler::FilterSampler(Filter filter, Allocator alloc)
: domain(Point2f(-filter.Radius()), Point2f(filter.Radius())),
f(int(32 * filter.Radius().x), int(32 * filter.Radius().y), alloc),
distrib(alloc) {
for (int y = 0; y < f.YSize(); ++y)
for (int x = 0; x < f.XSize(); ++x) {
Point2f p = domain.Lerp(Point2f((x + 0.5f) / f.XSize(),
(y + 0.5f) / f.YSize()));
f(x, y) = filter.Evaluate(p);
}
distrib = PiecewiseConstant2D(f, domain, alloc);
}这里将f初始化为filter.Radius的32倍,并根据x和y坐标依次填充其中的filter值,这里相当于在filter的x和y方向上每个单位采样了32这个样本,比如filter.Radius.x=2,f.XSize()就为64,计算点的时候使用的是 (索引 + 0.5) / 64,保证2个单位上均匀分布了64个样本点。
distrib是一个PiecewiseConstant2D,接受f和domin作为参数(alloc是分配器),可以理解为它接受了filter的重要信息,后面可以通过一个二维随机数来采样出filter的值和对应的pdf。
FilterSampler的采样函数:
FilterSample Sample(Point2f u) const {
Float pdf;
Point2i pi;
Point2f p = distrib.Sample(u, &pdf, &pi);
return FilterSample{p, f[pi] / pdf};
}BOX Filter
盒型滤波器(box filter)是一个最常用的滤波器,它的实现很简单,在它的滤波区域内所有采样的权重都是一样的。图a就是一个盒型滤波器的示意图。

盒型滤波器在低频的信号有更好的效果,但在高频信号中,盒型滤波器往往会导致一些失真,

因为它的重建是将周围的采样信号值“平均”后计算得到当前点的值,在高频的信号中这个方法误差比较大。
box filter的实现:
class BoxFilter {
public:
...
private:
Vector2f radius;
};成员变量只有一个radius。
Evaluate函数:
Float Evaluate(Point2f p) const {
return (std::abs(p.x) <= radius.x && std::abs(p.y) <= radius.y) ? 1 : 0;
}在radius之内返回1,其余区域返回0。
Sample函数:
FilterSample Sample(Point2f u) const {
Point2f p(Lerp(u[0], -radius.x, radius.x),
Lerp(u[1], -radius.y, radius.y));
return {p, Float(1)};
}采样的点p通过在radius中根据u插值计算而来,weight(函数值 / pdf)永远为1,因为它是均匀分布的,pdf为常数,在任意一点处,f(p) = pdf(p) = 1 / integral(f)。
Integral函数:
Float Integral() const { return 2 * radius.x * 2 * radius.y; }返回filter所占的面积。
box filter相当于对radius中的所有像素点进行平均,这个操作将模糊整张图片,从重建的角度来分析,这就相当于将当前采样点的值与周围采样点的值进行一个平均的计算来估计那些未采样点的值,这样就可以减少采样不足带来的误差。
Triangle Filter
三角形滤波器的效果比盒型滤波器的效果稍好一些,因为它根据采样点的远近设置了不同的权重,滤波器边缘的采样点权重更小,中心的采样点权重更大。

图b就是三角形滤波器的示意图。
TriangleFilter的实现:
class TriangleFilter {
public:
...
private:
Vector2f radius;
};和box filter一样,它只有一个radius成员变量。
Evaluate函数:
Float Evaluate(Point2f p) const {
return std::max<Float>(0, radius.x - std::abs(p.x)) *
std::max<Float>(0, radius.y - std::abs(p.y));
}p点的函数值通过x和y两个方向的线性插值来计算,当p为边缘的点时,函数值为0,当p为原点时,函数值为radius.x * radius.y。
Sample函数:
FilterSample Sample(Point2f u) const {
return {Point2f(SampleTent(u[0], radius.x),
SampleTent(u[1], radius.y)), Float(1)};
}这里使用了SampleTent函数,它能够根据锥形的函数(上图b)进行采样,就像蒙特卡洛积分和采样中对线性插值函数进行采样一样(内部就是用两个线性插值来实现的)。这里返回的weight也是1,(由于现在不了解SampleTent的实现,不清楚采样出来的pdf与函数值的关系,这里就不深入分析)
Integral函数:
Float Integral() const { return Sqr(radius.x) * Sqr(radius.y); }返回滤波器在xy上的积分值(这个积分值是如何计算的,它底的面积应该是一个对角线等于2x和2y的棱形,高为xy,算出来的体积与这个积分值不同)。
Gaussian Filter
高斯滤波器的效果比上面两种滤波器的效果更好,它会轻微地模糊图像,但是可以减少锯齿。在了解高斯滤波器之前,先了解正态分布的高斯函数:
决定了函数曲线的中心,决定了函数的变化幅度,高斯函数的图像为:

高斯滤波器使用的滤波函数为:
将设置为0,表示函数的中心在y轴上,当x从0变化到r时,f(x)的值会从峰值缓慢变化至0。其中可以先进行预计算。
GaussianFilter函数的实现:
class GaussianFilter {
public:
GaussianFilter(Vector2f radius, Float sigma = 0.5f, Allocator alloc = {})
: radius(radius), sigma(sigma), expX(Gaussian(radius.x, 0, sigma)),
expY(Gaussian(radius.y, 0, sigma)), sampler(this, alloc) {}
...
private:
Vector2f radius; // 滤波器半径
Float sigma, expX, expY; // sigma值和g(r,0,\sigma)的预计算值
FilterSampler sampler; // FilterSampler对象,用于从滤波函数中采样值,由于GaussianFilter比较复杂,所以需要使用这个辅助采样类
};Evaluate函数:
Float Evaluate(Point2f p) const {
return (std::max<Float>(0, Gaussian(p.x, 0, sigma) - expX) *
std::max<Float>(0, Gaussian(p.y, 0, sigma) - expY));
}计算滤波器函数值。
Integral函数:
Float Integral() const {
return ((GaussianIntegral(-radius.x, radius.x, 0, sigma) -
2 * radius.x * expX) *
(GaussianIntegral(-radius.y, radius.y, 0, sigma) -
2 * radius.y * expY));
}滤波器函数的积分值,使用如下方式计算:
分别计算x和y方向上的积分,然后相乘。
Sample函数:
FilterSample Sample(Point2f u) const { return sampler.Sample(u); }采样函数需要借助FilterSampler。