常用的反射模型

在反射模型章节中，介绍了渲染时光照反射的计算原理，包括镜面反射定律、折射定律、粗糙度和微平面理论等，并且给出了一个简单的漫反射（Diffuse Reflection）示例。由于篇幅原因，将常用的反射模型介绍拆分到这里，示例代码来源于PBRT书籍。
在BxDF接口设计中提到过，一个反射模型至少需要包含3个函数，f（在知道入射方向和出射方向的情况下计算BxDF的值）、Sample_f（在知道出射方向的情况下采样入射方向，并计算BxDF的值），PDF（该BxDF的分布函数）。
下面介绍一些常用的反射模型。

导体BRDF

金属导体有一个物理性质，进入金属的光线会被完全吸收，不会发生散射，所以金属导体只需要考虑反射即可，这也是导体使用的反射模型是BRDF的原因。

class ConductorBxDF {
  public:
    ...
  private:
    TrowbridgeReitzDistribution mfDistrib;
    SampledSpectrum eta, k;
};

其中有两个成员变量，mfDistrib描述粗糙度和微平面的分布，eta, k是折射率和衰减率，它们会被当做一个复数的实部和虚部来处理，在导体的菲涅尔方程有说明。

Sample_f

pstd::optional<BSDFSample>
Sample_f(Vector3f wo, Float uc, Point2f u, TransportMode mode,
         BxDFReflTransFlags sampleFlags = BxDFReflTransFlags::All) const {
    if (!(sampleFlags & BxDFReflTransFlags::Reflection)) return {};
    if (mfDistrib.EffectivelySmooth()) {
        // 镜面反射 
        Vector3f wi(-wo.x, -wo.y, wo.z);
        SampledSpectrum f = FrComplex(AbsCosTheta(wi), eta, k) / AbsCosTheta(wi);
        return BSDFSample(f, wi, 1, BxDFFlags::SpecularReflection);
    }
    // 微平面采样
    Vector3f wm = mfDistrib.Sample_wm(wo, u);
    Vector3f wi = Reflect(wo, wm);
    if (!SameHemisphere(wo, wi)) return {};
 
    // 微平面的 pdf 
    Float pdf = mfDistrib.PDF(wo, wm) / (4 * AbsDot(wo, wm));
 
    // 计算BRDF值
    Float cosTheta_o = AbsCosTheta(wo), cosTheta_i = AbsCosTheta(wi);
    SampledSpectrum F = FrComplex(AbsDot(wo, wm), eta, k);
 
    SampledSpectrum f = mfDistrib.D(wm) * F * mfDistrib.G(wo, wi) /
                           (4 * cosTheta_i * cosTheta_o);
    return BSDFSample(f, wi, pdf, BxDFFlags::GlossyReflection);
}

镜面但反射部分：

        Vector3f wi(-wo.x, -wo.y, wo.z);
        SampledSpectrum f = FrComplex(AbsCosTheta(wi), eta, k) / AbsCosTheta(wi);
        return BSDFSample(f, wi, 1, BxDFFlags::SpecularReflection);

由于计算时所有的方向都被转换到法线-切线的坐标空间，所以反射方向等于(-wo.x, -wo.y, wo.z)，不需要使用反射定律的函数计算了。
镜面反射只在反射方向上贡献光照效果，所以它的pdf是一个$\delta$分布函数，按照pdf的定义，它应该在0处（观察方向等于反射方向时）为无穷大，在其余地方为0。但是在使用时，“无穷大”的概念必然是要从计算机中程序规避的，所以这里设置pdf为1（相当于只有这种情况对积分有贡献）。在根据蒙特卡洛积分的计算，单次采样时有

$$\frac{f_r(p,{\omega }_o,{\omega }_i)L_i({\omega }_i)cos{\theta }_i}{1}=F({\omega }_r)L_i({\omega }_r)$$

由于是完美镜面反射，两边的$L_i$是相等的，于是

$$f_r(p,{\omega }_o,{\omega }_i)=\frac{F({\omega }_r)}{cos{\theta }_i}=\frac{F({\omega }_r)}{cos{\theta }_r}$$

也就是上面的计算方法。在完美镜面情况下，透射与反射的计算方式相同。
后续的微平面采样、pdf计算、BRDF使用的都是Torrance–Sparrow模型中的方法。

f

SampledSpectrum f(Vector3f wo, Vector3f wi, TransportMode mode) const {
    if (!SameHemisphere(wo, wi)) return {};
    // 镜面反射时这个函数不提供任何值
    if (mfDistrib.EffectivelySmooth()) return {};
    
    // 在已知wi和wo的情况下计算wm
    Float cosTheta_o = AbsCosTheta(wo), cosTheta_i = AbsCosTheta(wi);
    if (cosTheta_i == 0 || cosTheta_o == 0) return {};
    Vector3f wm = wi + wo;
    if (LengthSquared(wm) == 0) return {};
    wm = Normalize(wm);
 
    // 和上面相同的BRDF计算方法 
    SampledSpectrum F = FrComplex(AbsDot(wo, wm), eta, k);
 
    return mfDistrib.D(wm) * F * mfDistrib.G(wo, wi) /
              (4 * cosTheta_i * cosTheta_o);
}

这里wm和BRDF的计算方式在Torrance–Sparrow模型中也介绍过。
重点在于镜面反射，当发生镜面反射时这个函数不提供任何值，按照上面的结论，它这里提供的pdf应该是0，但是在计算机程序中，后面使用采样结果除以pdf时必然会除以0。所以这里按照镜面反射的物理定义，当观察方向与反射方向不一致时（只要不是严格的从wo使用反射定律计算wi，都视为不一致），它的光照贡献都为0，所以这里直接返回”空值”。

pdf

Float PDF(Vector3f wo, Vector3f wi, TransportMode mode,
          BxDFReflTransFlags sampleFlags) const {
    if (!(sampleFlags & BxDFReflTransFlags::Reflection)) return 0;
    if (!SameHemisphere(wo, wi)) return 0;
    if (mfDistrib.EffectivelySmooth()) return 0;
    
       Vector3f wm = wo + wi;
       if (LengthSquared(wm) == 0) return 0;
       wm = FaceForward(Normalize(wm), Normal3f(0, 0, 1)); 
       return mfDistrib.PDF(wo, wm) / (4 * AbsDot(wo, wm));
}
 
template <typename T>
Normal3<T> FaceForward(Normal3<T> n, Vector3<T> v) {
    return (Dot(n, v) < 0.f) ? -n : n;
}

pdf的计算方式上面已介绍。

绝缘体BSDF

相比于金属导体，光线在绝缘体上同时会发生反射和透射，所以它的反射模型也更加复杂。

class DielectricBxDF {
  public:
    ...
  private:
    Float eta;
    TrowbridgeReitzDistribution mfDistrib;
};

绝缘体不需要考虑光线在物体内部的散射效果，所以只有折射率。

Sample_f

光滑的绝缘体

pstd::optional<BSDFSample>
DielectricBxDF::Sample_f(Vector3f wo, Float uc, Point2f u,
        TransportMode mode, BxDFReflTransFlags sampleFlags) const {
    if (eta == 1 || mfDistrib.EffectivelySmooth()) {
        // 镜面反射
        Float R = FrDielectric(CosTheta(wo), eta), T = 1 - R;
        // 计算发生反射和透射的概率
        Float pr = R, pt = T;
        if (!(sampleFlags & BxDFReflTransFlags::Reflection)) pr = 0;
        if (!(sampleFlags & BxDFReflTransFlags::Transmission)) pt = 0;
        if (pr == 0 && pt == 0)
            return {};
 
        if (uc < pr / (pr + pt)) {
            Vector3f wi(-wo.x, -wo.y, wo.z);
            SampledSpectrum fr(R / AbsCosTheta(wi));
            return BSDFSample(fr, wi, pr / (pr + pt), BxDFFlags::SpecularReflection);
        } else {
            Vector3f wi;
            Float etap;
            bool valid = Refract(wo, Normal3f(0, 0, 1), eta, &etap, &wi);
            if (!valid) return {};
 
            SampledSpectrum ft(T / AbsCosTheta(wi));
            // 考虑非对称的散射和折射
            if (mode == TransportMode::Radiance)
                ft /= Sqr(etap);
 
            return BSDFSample(ft, wi, pt / (pr + pt),
                              BxDFFlags::SpecularTransmission, etap);
        }
    } else {
        ...
    }
}

光滑的绝缘体不需要考虑微表面分布，反射部分是镜面反射。
通过折射率计算反射和透射光线的能量比例，

        Float R = FrDielectric(CosTheta(wo), eta), T = 1 - R;
        Float pr = R, pt = T;

使用菲涅尔方程中的方法计算出反射能量占比R，在计算出透射能量占比T，以它们作为概率决定此次采样是反射还是透射。
镜面反射的计算方式和上面金属BRDF的一致，唯一的区别就是这次的pdf = pr / (pr + pt)，也就是发生反射的概率。
透射部分使用了折射定律介绍的方法，

        bool valid = Refract(wo, Normal3f(0, 0, 1), eta, &etap, &wi);
        if (!valid) return {};

这里的输出器etap和wi，wi是折射的方向，etap是折射率，在正常情况下etap=eta，只有发生的反向的折射时（即入射方向和法线不在同一侧，光线由物体内部射出），etap=1 / eta。
下面折射光线BSDF值的计算也和反射一样，但是多了一个步骤：

        if (mode == TransportMode::Radiance)
            ft /= Sqr(etap);

这里是考虑到真实世界的透射，透射是不对称的，当发生透射后，透射出的能量会出现衰减，

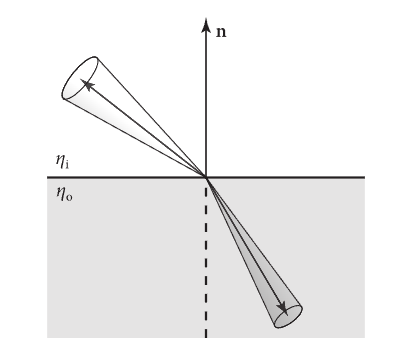
具体的关系为：

$$L_o=L_i\frac{{\eta }_o^2}{{\eta }_i^2}$$

因为代码中$eta={\eta }_o/{\eta }_i$，所以这里计算Li时要除以sqr(eta)。
这种透射方式对路径追踪来说很不友好，因为整个路径追踪算法都是按照光路是可逆的这一定律来设计的，所以在一些渲染系统中，会直接忽悠掉透射能量的衰减，这里也加了条件，TransportMode为Radiance时才会考虑不对称透射的情况。

粗糙的绝缘体

粗糙的绝缘体在反射时需要考虑微平面理论，并且在透射时计算方式也有差异。

pstd::optional<BSDFSample>
DielectricBxDF::Sample_f(Vector3f wo, Float uc, Point2f u,
        TransportMode mode, BxDFReflTransFlags sampleFlags) const {
        ...
        }
    } else {
        // 采样微平面法线
        Vector3f wm = mfDistrib.Sample_wm(wo, u);
        Float R = FrDielectric(Dot(wo, wm), eta);
        Float T = 1 - R;
 
        Float pr = R, pt = T;
        if (!(sampleFlags & BxDFReflTransFlags::Reflection)) pr = 0;
        if (!(sampleFlags & BxDFReflTransFlags::Transmission)) pt = 0;
        if (pr == 0 && pt == 0)
            return {};
 
        Float pdf;
        if (uc < pr / (pr + pt)) {
            Vector3f wi = Reflect(wo, wm);
            if (!SameHemisphere(wo, wi)) return {};
            pdf = mfDistrib.PDF(wo, wm) / (4 * AbsDot(wo, wm)) * pr / (pr + pt);
            
            SampledSpectrum f(mfDistrib.D(wm) * mfDistrib.G(wo, wi) * R /
                                    (4 * CosTheta(wi) * CosTheta(wo)));
            return BSDFSample(f, wi, pdf, BxDFFlags::GlossyReflection);
        } else {
            Float etap;
            Vector3f wi;
            bool tir = !Refract(wo, (Normal3f)wm, eta, &etap, &wi);
            if (SameHemisphere(wo, wi) || wi.z == 0 || tir)
                return {};
 
            Float denom = Sqr(Dot(wi, wm) + Dot(wo, wm) / etap);
            Float dwm_dwi = AbsDot(wi, wm) / denom;
            pdf = mfDistrib.PDF(wo, wm) * dwm_dwi * pt / (pr + pt);
 
            SampledSpectrum ft(T * mfDistrib.D(wm) * mfDistrib.G(wo, wi) *
                         std::abs(Dot(wi, wm) * Dot(wo, wm) /
                         (CosTheta(wi) * CosTheta(wo) * denom)));
 
            if (mode == TransportMode::Radiance)
                    ft /= Sqr(etap);
 
            return BSDFSample(ft, wi, pdf, BxDFFlags::GlossyTransmission, etap);
        }
    }
}

反射的部分与粗糙金属导体材质的反射相似，增加了一个反射概率pr / (pr + pt)到pdf。
主要区别在与透射部分。
第一个区别，不在考虑全反射的透射，上面的光滑绝缘体允许Refract函数计算出的wi和wo在同一侧，而这里当它们位于同一侧是直接返回空。

            bool tir = !Refract(wo, (Normal3f)wm, eta, &etap, &wi);
            if (SameHemisphere(wo, wi) || wi.z == 0 || tir)
                return {};

第二，BSDF的计算方式发生改变，由于反射和透射的区别，计算BSDF时不能继续按照半角向量中使用的方法，其$d{\omega }_m$与$d{\omega }_i$的关系发生了改变，具体的关系为：

$$\begin{array}{rl}d{\omega }_m& =\frac{{\eta }_i^2|{\omega }_i\cdot {\omega }_m|}{({\eta }_i({\omega }_i\cdot {\omega }_m)+{\eta }_o({\omega }_o\cdot {\omega }_m){)}^2}d{\omega }_i\\ & =\frac{|{\omega }_o\cdot {\omega }_m|}{(({\omega }_i\cdot {\omega }_m)+({\omega }_o\cdot {\omega }_m)/\eta {)}^2}d{\omega }_i\end{array}$$

于是PDF中计算BSDF的pdf就变成了

$$p({\omega }_i)=D_{{\omega }_o}({\omega }_m)\frac{d{\omega }_m}{d{\omega }_i}=\frac{D_{{\omega }_o}({\omega }_m)|{\omega }_o\cdot {\omega }_m|}{(({\omega }_i\cdot {\omega }_m)+({\omega }_o\cdot {\omega }_m)/\eta {)}^2}$$

对应的代码：

            Float denom = Sqr(Dot(wi, wm) + Dot(wo, wm) / etap);
            Float dwm_dwi = AbsDot(wi, wm) / denom;
            pdf = mfDistrib.PDF(wo, wm) * dwm_dwi * pt / (pr + pt);

BSDF值的计算由于pdf的改变也发生改变，具体的推导过程与Torrance–Sparrow BRDF相似，这里直接给出结果：

$$f_t(p,{\omega }_o,{\omega }_i)=\frac{D({\omega }_m)(1-F({\omega }_o\cdot {\omega }_m))G({\omega }_i,{\omega }_o)}{(({\omega }_i\cdot {\omega }_m)+({\omega }_o\cdot {\omega }_m)/\eta {)}^2}\frac{|{\omega }_i\cdot {\omega }_m||{\omega }_o\cdot {\omega }_m|}{|cos{\theta }_i||cos{\theta }_o|}$$

对应的代码

            SampledSpectrum ft(T * mfDistrib.D(wm) * mfDistrib.G(wo, wi) *
                         std::abs(Dot(wi, wm) * Dot(wo, wm) /
                         (CosTheta(wi) * CosTheta(wo) * denom)));

f

这里也发光滑和粗糙绝缘体，和光滑金属一样，光滑绝缘体f返回0。

SampledSpectrum DielectricBxDF::f(Vector3f wo, Vector3f wi,
                                  TransportMode mode) const {
    if (eta == 1 || mfDistrib.EffectivelySmooth())
        return SampledSpectrum(0.f);
 
    Float cosTheta_o = CosTheta(wo), cosTheta_i = CosTheta(wi);
    // cosTheta同号，证明wi和wo在同一侧，发生反射
    bool reflect = cosTheta_i * cosTheta_o > 0;
    float etap = 1;
    // 如果发生透射，确认透射的方向
    if (!reflect)
        etap = cosTheta_o > 0 ? eta : (1 / eta);
    // 计算wm
    Vector3f wm = wi * etap + wo;
    if (cosTheta_i == 0 || cosTheta_o == 0 || LengthSquared(wm) == 0) return {};
    wm = FaceForward(Normalize(wm), Normal3f(0, 0, 1));
 
    // 忽略背向微平面
    if (Dot(wm, wi) * cosTheta_i < 0 || Dot(wm, wo) * cosTheta_o < 0)
        return {};
 
    Float F = FrDielectric(Dot(wo, wm), eta);
    if (reflect) {
        // 反射BSDF
        return SampledSpectrum(mfDistrib.D(wm) * mfDistrib.G(wo, wi) * F /
                                     std::abs(4 * cosTheta_i * cosTheta_o));
    } else {
        // 透射BSDF
        Float denom = Sqr(Dot(wi, wm) + Dot(wo, wm)/etap) * cosTheta_i * cosTheta_o;
        Float ft = mfDistrib.D(wm) * (1 - F) * mfDistrib.G(wo, wi) *
                         std::abs(Dot(wi, wm) * Dot(wo, wm) / denom);
        if (mode == TransportMode::Radiance)
            ft /= Sqr(etap);
 
        return SampledSpectrum(ft);
    }
}

这里的重点在于wm的计算，根据折射定律，wm的计算规则如下，

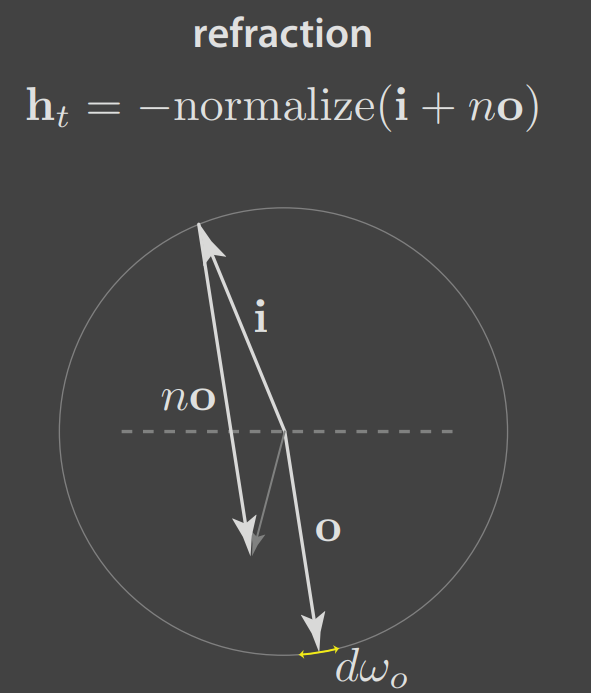
使用公式表示：

$${\omega }_m=\frac{{\eta }_i{\omega }_i+{\eta }_o{\omega }_o}{|{\eta }_i{\omega }_i+{\eta }_o{\omega }_o|}=\frac{\eta {\omega }_i+{\omega }_o}{|\eta {\omega }_i+{\omega }_o|}$$

公式里的${\omega }_i$和${\omega }_o$与图中是相反的，因为图里面是按照正常的光路，${\omega }_i$为入射方向，${\omega }_o$为出射方向，但是在PBRT的光线追踪里面，光路是相反的，所以这两个方向的含义是相反的。
计算wm的方式：

    Vector3f wm = wi * etap + wo;
    if (cosTheta_i == 0 || cosTheta_o == 0 || LengthSquared(wm) == 0) return {};
    // 这里传入的wm是Normalize的
    wm = FaceForward(Normalize(wm), Normal3f(0, 0, 1));

FaceForward定义如下

template <typename T>
Normal3<T> FaceForward(Normal3<T> n, Vector3<T> v) {
    return (Dot(n, v) < 0.f) ? -n : n;
}

保证wm的方向与宏观法线在同一侧。
计算出wm后，和之前一样，需要保证wm与宏观表面的法线是在同一侧的，因为需要忽略背向的微平面。

    if (Dot(wm, wi) * cosTheta_i < 0 || Dot(wm, wo) * cosTheta_o < 0)
        return {};

通过保证wi（或wo）与wm的夹角cos值与wi（或wo）与宏观法线的夹角cos值同号来保证wm与宏观法线方向一致。
后续反射和透射的BSDF值计算与Sample_f相同。

pdf

Float DielectricBxDF::PDF(Vector3f wo, Vector3f wi, TransportMode mode,
          BxDFReflTransFlags sampleFlags) const {
    // 镜面反射依然返回0
    if (eta == 1 || mfDistrib.EffectivelySmooth())
        return 0;
 
    // 计算微平面法线，并以此计算菲涅尔项
    Float cosTheta_o = CosTheta(wo), cosTheta_i = CosTheta(wi);
    bool reflect = cosTheta_i * cosTheta_o > 0;
    float etap = 1;
    if (!reflect)
        etap = cosTheta_o > 0 ? eta : (1 / eta);
    Vector3f wm = wi * etap + wo;
    if (cosTheta_i == 0 || cosTheta_o == 0 || LengthSquared(wm) == 0) return {};
    wm = FaceForward(Normalize(wm), Normal3f(0, 0, 1));
 
    if (Dot(wm, wi) * cosTheta_i < 0 || Dot(wm, wo) * cosTheta_o < 0)
        return {};
 
    Float R = FrDielectric(Dot(wo, wm), eta);
    Float T = 1 - R;
 
    Float pr = R, pt = T;
    if (!(sampleFlags & BxDFReflTransFlags::Reflection)) pr = 0;
    if (!(sampleFlags & BxDFReflTransFlags::Transmission)) pt = 0;
    if (pr == 0 && pt == 0)
        return {};
 
    Float pdf;
    if (reflect) {
        pdf = mfDistrib.PDF(wo, wm) / (4 * AbsDot(wo, wm)) * pr / (pr + pt);
    } else {
        Float denom = Sqr(Dot(wi, wm) + Dot(wo, wm) / etap);
        Float dwm_dwi = AbsDot(wi, wm) / denom;
        pdf = mfDistrib.PDF(wo, wm) * dwm_dwi * pt / (pr + pt);
    }
    return pdf;
}

pdf的计算方式在上面已经介绍过了，没有新的概念，不再赘述。

薄绝缘体BSDF

薄的绝缘体和普通绝缘体的反射模型有着较大差异，由于物体较薄，透射的光线会在物体内部反射后回到物体表面，这就导致反射的能量比菲涅尔方程计算出的要大。下面是一个薄绝缘体反射模型的示意图。

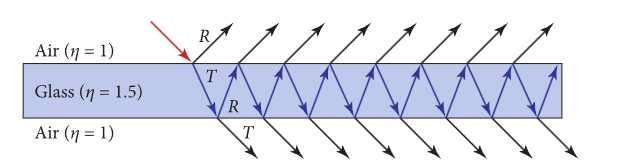
光线在物体内部不断发生弹射，导致反射出的光线增多。
最终反射的光线能量计算，

$$R^{\prime }=R+TRT+TRRRT+...=R+\frac{T^{2}R}{1-R^2}$$

根据能量守恒定律，透射光线的能量为

$$T’=1-R^{\prime }$$

它的BSDF定义：

class ThinDielectricBxDF {
  public:
    ...
  private:
    Float eta;
};

薄的绝缘体不再考虑粗糙度和微平面，假设它们都是光滑的镜面（比如玻璃片、塑料袋），所以成员变量中只有折射率eta。

Sample_f

pstd::optional<BSDFSample>
Sample_f(Vector3f wo, Float uc, Point2f u, TransportMode mode,
         BxDFReflTransFlags sampleFlags) const {
    Float R = FrDielectric(AbsCosTheta(wo), eta), T = 1 - R;
    if (R < 1) {
        R += Sqr(T) * R / (1 - Sqr(R));
        T = 1 - R;
    }
 
    Float pr = R, pt = T;
    if (!(sampleFlags & BxDFReflTransFlags::Reflection)) pr = 0;
    if (!(sampleFlags & BxDFReflTransFlags::Transmission)) pt = 0;
    if (pr == 0 && pt == 0)
        return {};
 
    if (uc < pr / (pr + pt)) {
        Vector3f wi(-wo.x, -wo.y, wo.z);
        SampledSpectrum fr(R / AbsCosTheta(wi));
        return BSDFSample(fr, wi, pr / (pr + pt), BxDFFlags::SpecularReflection);
    } else {
        Vector3f wi = -wo;
        SampledSpectrum ft(T / AbsCosTheta(wi));
        return BSDFSample(ft, wi, pt / (pr + pt), BxDFFlags::SpecularTransmission);
    }
}

增加了一个步骤，使用FrDielectric计算出R和T之后，如果R<1，也就是会同时发生反射和透射，那么其R和T需要上面的公式重新计算，

    if (R < 1) {
        R += Sqr(T) * R / (1 - Sqr(R));
        T = 1 - R;
    }

还有一个需要注意的是透射光方向的计算，

    Vector3f wi = -wo;

透射光方向为入射光方向的反方向，这个从上面的示意图中可以看出，由于发生了两次折射，光线的方向并没有发生变化，所以可以直接取入射光的反方向。严格来说，透射出的光线和入射光方向是有一定偏移的，这里做了简化，忽略了这种偏移。
这里取反的原因是，在程序中，为了方便计算，所有的光线方向定义都是从物体出发，比如物体到光源，物体到相机。

f

由于是完美的镜面反射，BSDF值返回0，上面f章节有解释。

       SampledSpectrum f(Vector3f wo, Vector3f wi, TransportMode mode) const {
           return SampledSpectrum(0);
       }

pdf

镜面反射，pdf函数直接返回0，

       Float PDF(Vector3f wo, Vector3f wi, TransportMode mode,
                 BxDFReflTransFlags sampleFlags) const {
           return 0;
       }