disney BRDF和disney BSDF

反射模型和常用的反射模型中已经将渲染中PBR的机制和实现方案了解得差不多了。然而在应用中，这套PBR方案应用并不广泛。观察可以发现，PBR中的概念和参数繁多且复杂，并且并不灵活，需要考虑一个物体是导体还是绝缘体，需要考虑物体进行的是镜面反射还是漫反射，亦或是有粗糙度的微平面反射，并且这些不同类型的BxDF实现方案差异巨大。
disney BRDF是目前应用最为广泛的反射模型，几乎所有渲染器都支持此模型，或者以此为基础进行扩展。
顾名思义disney BRDF是BRDF模型，所以主要考虑的是光线的反射，对于光线的透射使用了一些近似方案来模拟，它也非常适合用于实时渲染领域。

disney BRDF的理念

disney BRDF核心理念如下（直接贴了毛星云大佬的总结，disney BRDF原文章里也有介绍）：

• 应使用直观的参数，而不是物理类的晦涩参数。
• 参数应尽可能少。
• 参数在其合理范围内应该为0到1。
• 允许参数在有意义时超出正常的合理范围。
• 所有参数组合应尽可能健壮和合理。
  其注重实用性大于物体正确性，对美术更加友好。

下面是disney BRDF的参数（使用metallic-roughness工作流）：

• baseColor（固有色）：表面颜色，通常由纹理贴图提供。
• subsurface（次表面）：使用次表面近似控制漫反射形状。
• metallic（金属度）：金属（0 = 电介质，1 =金属）。这是两种不同模型之间的线性混合。金属模型没有漫反射成分，并且还具有等于基础色的着色入射镜面反射。
• specular（镜面反射强度）：入射镜面反射量。用于取代折射率。
• specularTint（镜面反射颜色）：对美术控制的让步，用于对基础色（basecolor）的入射镜面反射进行颜色控制。掠射镜面反射仍然是非彩色的。
• roughness（粗糙度）：表面粗糙度，控制漫反射和镜面反射。
• anisotropic（各向异性强度）：各向异性程度。用于控制镜面反射高光的纵横比。（0 =各向同性，1 =最大各向异性。）
• sheen（光泽度）：一种额外的掠射分量（grazing component），主要用于布料。
• sheenTint（光泽颜色）：对sheen（光泽度）的颜色控制，也是一个美术参数。
• clearcoat（清漆强度）：有特殊用途的第二个镜面波瓣（specular lobe）。
• clearcoatGloss（清漆光泽度）：控制透明涂层光泽度，0 = “缎面（satin）”外观，1 = “光泽（gloss）”外观。
  下面是官方提供的各参数效果示意图：
  

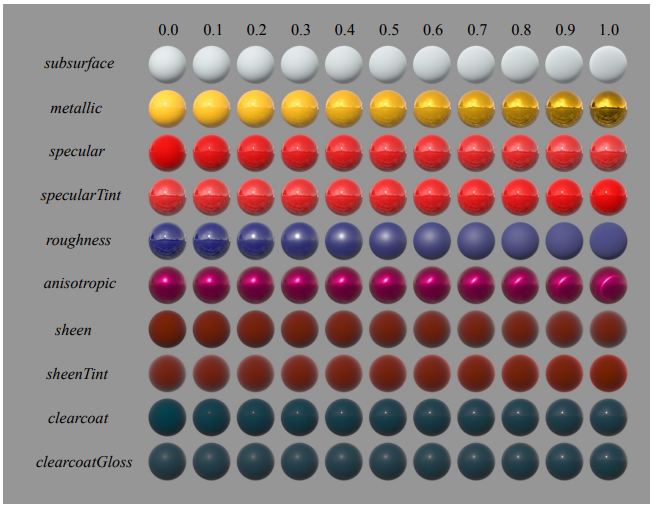
disney BRDF的实现原理

总览

disney BRDF由多种类型的BRDF混合而来，其实现原理图如下：

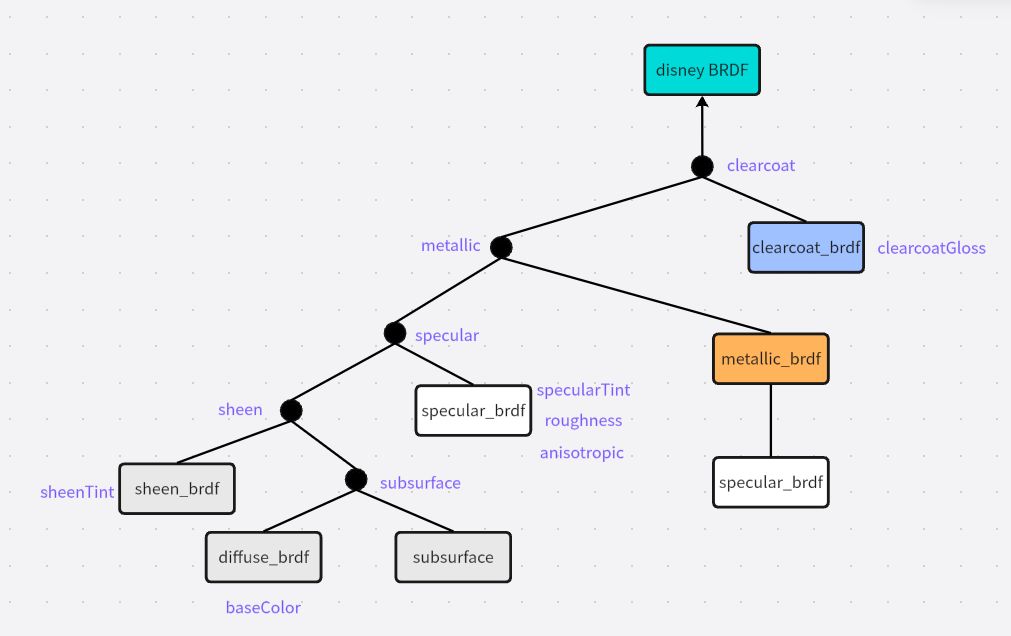
总体可以将其概括为DielectricBRDF与ConductorBRDF的混合，使用参数metallic控制混合比例。
对于DielectricBRDF，它由DiffuseBRDF和SpecularBRDF混合而来，依然使用Torrance–Sparrow BRDF的思想，即

$$f_r({\omega }_i,{\omega }_o)=f_{diffuse}+\frac{D({\omega }_h)F({\omega }_h,{\omega }_o)G({\omega }_i,{\omega }_o)}{4\cos {\theta }_i\cos {\theta }_o}$$

对于ConductorBRDF，它只包含specular部分，因为金属材质吸收光线能力强，不再发生漫反射和次表面散射。
为了方便，下面使用金属和非金属来表示导体和绝缘体。

下面是disney BRDF的官方实现示例（disney_brdf）:

# variables go here...
# [type] [name] [min val] [max val] [default val]
::begin parameters
color baseColor .82 .67 .16
float metallic 0 1 0
float subsurface 0 1 0
float specular 0 1 .5
float roughness 0 1 .5
float specularTint 0 1 0
float anisotropic 0 1 0
float sheen 0 1 0
float sheenTint 0 1 .5
float clearcoat 0 1 0
float clearcoatGloss 0 1 1
::end parameters


::begin shader

const float PI = 3.14159265358979323846;

float sqr(float x) { return x*x; }

float SchlickFresnel(float u)
{
    float m = clamp(1-u, 0, 1);
    float m2 = m*m;
    return m2*m2*m; // pow(m,5)
}

float GTR1(float NdotH, float a)
{
    if (a >= 1) return 1/PI;
    float a2 = a*a;
    float t = 1 + (a2-1)*NdotH*NdotH;
    return (a2-1) / (PI*log(a2)*t);
}

float GTR2(float NdotH, float a)
{
    float a2 = a*a;
    float t = 1 + (a2-1)*NdotH*NdotH;
    return a2 / (PI * t*t);
}

float GTR2_aniso(float NdotH, float HdotX, float HdotY, float ax, float ay)
{
    return 1 / (PI * ax*ay * sqr( sqr(HdotX/ax) + sqr(HdotY/ay) + NdotH*NdotH ));
}

float smithG_GGX(float NdotV, float alphaG)
{
    float a = alphaG*alphaG;
    float b = NdotV*NdotV;
    return 1 / (NdotV + sqrt(a + b - a*b));
}

float smithG_GGX_aniso(float NdotV, float VdotX, float VdotY, float ax, float ay)
{
    return 1 / (NdotV + sqrt( sqr(VdotX*ax) + sqr(VdotY*ay) + sqr(NdotV) ));
}

vec3 mon2lin(vec3 x)
{
    return vec3(pow(x[0], 2.2), pow(x[1], 2.2), pow(x[2], 2.2));
}


vec3 BRDF( vec3 L, vec3 V, vec3 N, vec3 X, vec3 Y )
{
    float NdotL = dot(N,L);
    float NdotV = dot(N,V);
    if (NdotL < 0 || NdotV < 0) return vec3(0);

    vec3 H = normalize(L+V);
    float NdotH = dot(N,H);
    float LdotH = dot(L,H);

    vec3 Cdlin = mon2lin(baseColor);
    float Cdlum = .3*Cdlin[0] + .6*Cdlin[1]  + .1*Cdlin[2]; // luminance approx.

    vec3 Ctint = Cdlum > 0 ? Cdlin/Cdlum : vec3(1); // normalize lum. to isolate hue+sat
    vec3 Cspec0 = mix(specular*.08*mix(vec3(1), Ctint, specularTint), Cdlin, metallic);
    vec3 Csheen = mix(vec3(1), Ctint, sheenTint);

    // Diffuse fresnel - go from 1 at normal incidence to .5 at grazing
    // and mix in diffuse retro-reflection based on roughness
    float FL = SchlickFresnel(NdotL), FV = SchlickFresnel(NdotV);
    float Fd90 = 0.5 + 2 * LdotH*LdotH * roughness;
    float Fd = mix(1.0, Fd90, FL) * mix(1.0, Fd90, FV);

    // Based on Hanrahan-Krueger brdf approximation of isotropic bssrdf
    // 1.25 scale is used to (roughly) preserve albedo
    // Fss90 used to "flatten" retroreflection based on roughness
    float Fss90 = LdotH*LdotH*roughness;
    float Fss = mix(1.0, Fss90, FL) * mix(1.0, Fss90, FV);
    float ss = 1.25 * (Fss * (1 / (NdotL + NdotV) - .5) + .5);

    // specular
    float aspect = sqrt(1-anisotropic*.9);
    float ax = max(.001, sqr(roughness)/aspect);
    float ay = max(.001, sqr(roughness)*aspect);
    float Ds = GTR2_aniso(NdotH, dot(H, X), dot(H, Y), ax, ay);
    float FH = SchlickFresnel(LdotH);
    vec3 Fs = mix(Cspec0, vec3(1), FH);
    float Gs;
    Gs  = smithG_GGX_aniso(NdotL, dot(L, X), dot(L, Y), ax, ay);
    Gs *= smithG_GGX_aniso(NdotV, dot(V, X), dot(V, Y), ax, ay);

    // sheen
    vec3 Fsheen = FH * sheen * Csheen;

    // clearcoat (ior = 1.5 -> F0 = 0.04)
    float Dr = GTR1(NdotH, mix(.1,.001,clearcoatGloss));
    float Fr = mix(.04, 1.0, FH);
    float Gr = smithG_GGX(NdotL, .25) * smithG_GGX(NdotV, .25);

    return ((1/PI) * mix(Fd, ss, subsurface)*Cdlin + Fsheen)
        * (1-metallic)
        + Gs*Fs*Ds + .25*clearcoat*Gr*Fr*Dr;
}

::end shader

这里将其一步步拆分，详细研究它的实现原理。

计算brdf颜色分量（反射率R，F0）

漫反射的颜色，

vec3 Cdlin = mon2lin(baseColor);

vec3 mon2lin(vec3 x)
{
    return vec3(pow(x[0], 2.2), pow(x[1], 2.2), pow(x[2], 2.2));
}

对baseColor进行gamma校正的结果，因为渲染时颜色空间应为线性空间。

去除漫反射颜色的亮度信息，只保留色相和饱和度，因为后续镜面反射颜色的计算不需要亮度信息。

    float Cdlum = .3*Cdlin[0] + .6*Cdlin[1]  + .1*Cdlin[2]; // luminance approx.

    vec3 Ctint = Cdlum > 0 ? Cdlin/Cdlum : vec3(1); // normalize lum. to isolate hue+sat

镜面反射颜色，

vec3 Cspec0 = mix(specular*.08*mix(vec3(1), Ctint, specularTint), Cdlin, metallic);

这里做了两次混合，第一次根据specularTint混合vec3(1)和Ctint，这里用到了specularTint参数，它将对非金属的镜面反射颜色进行控制，当它为0时，非金属的镜面反射颜色为白色，这是物理正确的，当它为1时，非金属的镜面反射颜色为Ctint，即baseColor去掉亮度。
上面对specularTint参数已经做了说明，这是一个对美术进行让步的参数，如果严格按照物理正确，非金属的镜面反射颜色应该为白色，而有了这个参数就可以对其进行控制。
第二次混合是根据metallic参数对非金属的镜面反射颜色和Cdlin进行混合，这很好理解，对于金属来说，其镜面反射颜色与漫反射颜色是相同的。
需要注意的是，非金属的镜面反射颜色还有specular*.08这个系数，也就是使用specular参数来控制它的镜面反射强度。specular参数是用来代替折射率IOR的，如果没有这个参数，通常应该使用菲涅尔方程结合IOR来计算反射光线的强度。
0.08这个系数则是一个实验总结的系数，默认情况下IOR为1.5，此时使用菲涅尔方程计算出的反射比例F0应为0.04，这表示当光线沿法线方向入射时，物体会反射4%的能量（将ior=1.5和${\theta }_i={\theta }_o=0$带入菲涅尔方程可以计算出来）。specular参数的取值为0到1，默认为0.5，此时计算出的Cspec0正好就是0.04。所以系数0.08就是通过specular默认值和IOR默认值反推出来的。
从这里也可以看出，对于非金属，其F0应为0到0.08之间（忽略specularTint参数），对于金属，F0等于漫反射率R。

sheen颜色，它也属于漫反射

vec3 Csheen = mix(vec3(1), Ctint, sheenTint);

光泽的颜色，通过sheenTint控制，和specularTint是类似的。

这一步计算出来各个brdf的颜色以及反射率，包括漫反射率Cdlin（R），镜面反射率Cspec0（F0）。

diffuse

如果使用最简单的Lambertian漫反射，diffuse项很好计算，

diffuse = Cdlin / Pi;

然而disney中的漫反射更复杂一些，它的计算公式为，

$$f_d=\frac{baseColor}{\pi }(1+(F_{D90}-1)(1-\cos {\theta }_l{)}^5)(1+(F_{D90}-1)(1-\cos {\theta }_v{)}^5)$$

其中，

$$F_{D90}=0.5+2roughness{\cos }^2{\theta }_d$$

代码实现：

    float FL = SchlickFresnel(NdotL), FV = SchlickFresnel(NdotV);
    float Fd90 = 0.5 + 2 * LdotH*LdotH * roughness;
    float Fd = mix(1.0, Fd90, FL) * mix(1.0, Fd90, FV);


float SchlickFresnel(float u)
{
    float m = clamp(1-u, 0, 1);
    float m2 = m*m;
    return m2*m2*m; // pow(m,5)
}

这里并没有直接乘以$\frac{baseColor}{\pi }$，这项工作放到最后面来完成。

disney漫反射相比于Lambertian漫反射，引入了SchlickFresnel项，这是一个基于观察经验的漫反射模型，它在物体边缘有更亮的漫反射效果，并且引入粗糙度对漫反射的影响。关于它更详细的解释，可以参考【渲染】Disney BSDF 深度解析。

subsurface

次表面散射被看作是漫反射的一部分，可以理解为光线进入物体后，在物体内部弹射的现象。
这一项是从Hanrahan-Krueger brdf近似而来，模拟次表面散射的效果，其公式为

$$\begin{array}{rl}{f}_{ss}& =1.25((\frac{1}{\cos {\theta }_l\cos {\theta }_v}-0.5)F_{ss}+0.5)\\ F_{ss}& =(1+(F_{SS90}-1)(1-\cos {\theta }_l{)}^5)(1+(F_{SS90}-1)(1-\cos {\theta }_v{)}^5)\\ F_{SS90}& =rougnhess\ast {\cos }^2{\theta }_l\end{array}$$

实现代码：

    float Fss90 = LdotH*LdotH*roughness;
    float Fss = mix(1.0, Fss90, FL) * mix(1.0, Fss90, FV);
    float ss = 1.25 * (Fss * (1 / (NdotL + NdotV) - .5) + .5);

FL和FV在diffuse项已经计算出来了。

specular

specular项的计算依然使用微平面模型，在Torrance–Sparrow模型中已经做过介绍，但是在实时渲染时，考虑到性能因素，并不能使用功能那么复杂的分布函数。

Schlick Fresnel

这是用来代替菲涅尔项的近似函数，其形式为

$$F_{Schlick}=F_0+(1-F_0)(1-\cos {\theta }_d{)}^5$$

这是实时渲染领域使用得最广泛的菲涅尔函数了，其中F0在上面各颜色分量计算时介绍过，表示光线沿法线方向入射时反射能量比例，对于非金属默认是0.04。
这个函数在上面diffuse和subsurface计算时使用过其变体，只是1和F0的位置调换了，简单理解就是随着${\theta }_d$从0度变化到90度，$(1-\cos {\theta }_d{)}^5$从0变到1，物体反射的能量从F0变化到1，即光线沿法线方向入射时反射能量比例为F0，而光线以法线垂直方向入射时反射能量比例为1，正好对应掠射时发生全反射的物理现象。而diffuse和subsurface获取的能量是反射后剩余的，所以它们的变化趋势与$F_{Schlick}$函数相反，所以1和Fd90（或Fss90）的位置调换了。
disney BRDF使用SchlickFresnel函数加mix函数实现Schlick Fresnel，

    float FH = SchlickFresnel(LdotH);
    vec3 Fs = mix(Cspec0, vec3(1), FH);

法线分布函数 GTR

disney BRDF使用的法线分布函数是GTR分布，其具体形式如下：

$$D_{GTR}({\theta }_h)=\frac{(\gamma -1)({\alpha }^2-1)}{\pi (1-({\alpha }^2{)}^{1-\gamma })}\frac{1}{(1+({\alpha }^2-1){\cos }^2{\theta }_h{)}^{\gamma }}$$

其中参数$\gamma$用来控制函数的下降速度，$\gamma$越大，随着${\theta }_h$的增大，函数趋近0的速度越快，$\alpha$表示粗糙度。
通常情况下只会使用$\gamma =1$和$\gamma =2$两个函数，前者用来计算clearcoat的specular，后者用来计算物体材质的specular。
可以发现$\gamma =1$时该函数是未定义的，它被替换为如下形式，

$$D_{GT{R}_1}({\theta }_h)=\frac{{\alpha }^2-1}{\pi \log {\alpha }^2}\frac{1}{(1+({\alpha }^2-1){\cos }^2{\theta }_h)}$$

当$\gamma =2$时，它为以下形式，

$$D_{GT{R}_2}({\theta }_h)=\frac{{\alpha }^2}{\pi }\frac{1}{(1+({\alpha }^2-1){\cos }^2{\theta }_h{)}^2}$$

如果考虑各向异性，就使用微平面的法线分布函数中介绍的Trowbridge-Reitz模型，为了使算法更高效，其被替换成如下形式：

$$D_{GT{R}_{2}aniso}({\theta }_h)=\frac{1}{\pi }\frac{1}{{\alpha }_x{\alpha }_y}\frac{1}{((h\cdot x{)}^2/{\alpha }_x^2+(h\cdot y{)}^2/{\alpha }_y^2+(h\cdot n{)}^2{)}^2}$$

其中x和y表示该点的切线和副切线，它们与法线n组成一个正交基。
几个函数的实现如下：

float GTR1(float NdotH, float a)
{
    if (a >= 1) return 1/PI;
    float a2 = a*a;
    float t = 1 + (a2-1)*NdotH*NdotH;
    return (a2-1) / (PI*log(a2)*t);
}

float GTR2(float NdotH, float a)
{
    float a2 = a*a;
    float t = 1 + (a2-1)*NdotH*NdotH;
    return a2 / (PI * t*t);
}

float GTR2_aniso(float NdotH, float HdotX, float HdotY, float ax, float ay)
{
    return 1 / (PI * ax*ay * sqr( sqr(HdotX/ax) + sqr(HdotY/ay) + NdotH*NdotH ));
}

几何函数 Smith-GGX

Smith-GGX随粗糙度的变化更加平滑，其形式为

$$\begin{array}{r}G(l,v,h)=G_{GGX}(l)G_{GGX}(v)\\ G_{GGX}(v)=\frac{2(n\cdot v)}{(n\cdot v)+\sqrt{{\alpha }^2+(1-{\alpha }^2)(n\cdot v{)}^2}}\\ \alpha =(0.5+roughness/2{)}^2\end{array}$$

这个函数有一个特别的地方，它的分子是$2(n\cdot v)$，如果再将$G_{GGX}(l)$考虑进去，它的分子就变成了$4(n\cdot v)(n\cdot l)$，正好与Torrance–Sparrow模型的分母相同，所以此项可以直接约分。这也是使用Smith-GGX的优点之一，最终的光照计算不需要除以$4(n\cdot v)(n\cdot l)$，减少了计算量。
代码实现：

float smithG_GGX(float NdotV, float alphaG)
{
    float a = alphaG*alphaG;
    float b = NdotV*NdotV;
    return 1 / (NdotV + sqrt(a + b - a*b));
}

注意这里已经去掉分子了。
同时，它有一个各项异性的版本，

$$G(v)=\frac{2(n\cdot v)}{n\cdot v+\sqrt{(x\cdot v\ast {\alpha }_x{)}^2+(y\cdot v\ast {\alpha }_y{)}^2+(n\cdot v{)}^2}}$$

和法线分布函数一样，x和y表示其切线和副切线，对应实现如下：

float smithG_GGX_aniso(float NdotV, float VdotX, float VdotY, float ax, float ay)
{
    return 1 / (NdotV + sqrt( sqr(VdotX*ax) + sqr(VdotY*ay) + sqr(NdotV) ));
}

同样去掉分子。

specular的计算

有了上面三个函数，就可以计算brdf的specular部分了，

    // specular
    float aspect = sqrt(1-anisotropic*.9);
    float ax = max(.001, sqr(roughness)/aspect);
    float ay = max(.001, sqr(roughness)*aspect);
    float Ds = GTR2_aniso(NdotH, dot(H, X), dot(H, Y), ax, ay);
    float FH = SchlickFresnel(LdotH);
    vec3 Fs = mix(Cspec0, vec3(1), FH);
    float Gs;
    Gs  = smithG_GGX_aniso(NdotL, dot(L, X), dot(L, Y), ax, ay);
    Gs *= smithG_GGX_aniso(NdotV, dot(V, X), dot(V, Y), ax, ay);

首先通过anisotropic和roughness计算出不同方向的粗糙度ax，ay，然后使用它们计算其他3个函数。
Ds使用GTR2_aniso即GTR法线分布函数的各项异性版本计算。
Fs使用SchlickFresnel和mix插值计算。
Gs分为两个方向，分布计算光源方向和观察方向的遮蔽效果，都使用使用smithG_GGX_aniso函数。

sheen

光泽通常用来模拟天鹅绒、布料这类材质外表的光泽效果，它们通常拥有较大的掠射效应，材质边缘呈现出更强的光线反射效果。
其计算方式很简单：

vec3 Fsheen = FH * sheen * Csheen;

FH是SchlickFresnel项，即$(1-\cos {\theta }_l{)}^5$，然后乘以光泽强度和光泽颜色。

clearcoat

clearcoat可以视为物体材质上的第二个高光反射，具体的计算方法与specular相似，

    // clearcoat (ior = 1.5 -> F0 = 0.04)
    float Dr = GTR1(NdotH, mix(.1,.001,clearcoatGloss));
    float Fr = mix(.04, 1.0, FH);
    float Gr = smithG_GGX(NdotL, .25) * smithG_GGX(NdotV, .25);

clearcoat同样计算D、F、G三项，但是其中的有的参数被固定了。
计算Dr时使用各项同性的GTR1分布，但是使用clearcoatGloss代替了roughess，具体来说，
roughess = 1 - clearcoatGloss，并且这里保证其最小值不会小于0.001。
计算Fr时，F0被固定为0.04，对应常用的IOR = 1.5。
计算Gr时，使用各项同性的smithG_GGX，并且其粗糙度被固定为0.25。

最终BRDF计算

将上面所有的项组合为最终结果，

    return ((1/PI) * mix(Fd, ss, subsurface)*Cdlin + Fsheen)
        * (1-metallic)
        + Gs*Fs*Ds + .25*clearcoat*Gr*Fr*Dr;
}

在这里可以看到，漫反射项Fd和次表面散射项ss通过subsurface参数混合，这意味着它们的能量总和是固定的，最终的结果需要乘以Cdlin / PI（漫反射率）。
Fsheen作为漫反射的一部分加入漫反射项的计算结果。
漫反射项会乘以1 - metallic，这表示当金属度为1时，漫反射会全部消失，对应金属材质没有漫反射的物理特性。
后面的specular和clearcoat直接加上即可，对于clearcoat，这里加上了系数clearcoat来控制其效果强度，前面的0.25应该是固定的美术调节参数，防止clearcoat效果过强，因为clearcoat这一项是没有考虑能量守恒的。

disney BSDF

在disney BRDF后，disney又针对其做了扩充，提出了disney BSDF，相比与原来的BRDF，BSDF增加了透射部分，并且对于次表面散射部分有了更加完善的实现。
上面提到过，BRDF的反射模型主要分为两部分，金属与非金属，

而BSDF引入了新的透射BSDF，

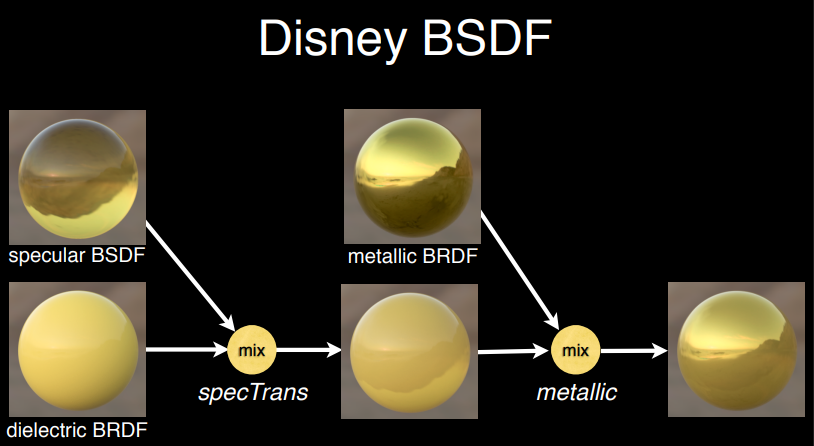
原本的dielectric BRDF需要和specular BSDF混合之后，才和metallic BRDF混合成最终BSDFF。

specular BSDF

作为新增项，specular BSDF引入了两个新参数：

• IOR：折射率，控制光线反射的能量比例，在BRDF中它由specular替代，现在需要计算透射部分，又将其使用回来。
• specTrans（Transmission）：控制透射光线能量比例，即透射效果强弱。
  在BSDF中，严格来说光线的能量被分为3部分，

$$\begin{array}{rl}\text{反射能量}& :E_{\text{refl}}=F\\ \text{透射能量}& :E_{\text{trans}}=(1-F)\cdot \text{specTrans}\\ \text{散射能量}& :E_{\text{sss}}=(1-F)\cdot (1-\text{specTrans})\end{array}$$

反射的能量F由菲涅尔定律计算出。
透射的能量为反射剩余的能量乘以specTrans系数。
最终剩下散射的能量，包括次表面散射部分和漫反射部分。
按照这个思路，specular BSDF将与diffuse + subsurface部分根据specTrans参数进行融合。
关于specular BSDF的计算方法，在粗糙的绝缘体中有推导，同样使用了微平面的理论。
specular BSDF只会在离线渲染中使用，第一，其计算方法太复杂，第二，只有在光线追踪算法中，才可以模拟光线透过物体时的渲染效果，在实时渲染中通常只使用alpha来实现半透明效果，要想实现更丰富的透射效果（如光线折射，磨砂玻璃），需要使用其他的技术手段模拟。

subsurface

Reference

https://zhuanlan.zhihu.com/p/60977923